题目内容
(本小题满分10分)选修4—5:不等式选讲
设函数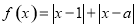 .
.
(1)若 时,解不等式
时,解不等式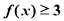 ;
;
(2)如果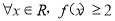 ,求
,求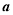 的取值范围
的取值范围
(1) ;
;
(2)(-∞,-1]∪[3,+∞).
【解析】
试题分析:【解析】
(1)当a=-1时,f(x)=︱x-1︳+︱x+1︳.由f(x)≥3得︱x-1︳+︱x+1|≥3
由绝对值的几何意义知不等式的解集为
若a=1,则f(x)=2|x-1|不满足题设条件.
若a<1, ,f(x)的最小值为1-a;
,f(x)的最小值为1-a;
若a>1, ,f(x)的最小值a-1.
,f(x)的最小值a-1.
所以对于任意x∈R,f(x)≥2的充要条件是|a-1|≥2,从而a的取值范围(-∞,-1]∪[3,+∞).
解析二
同上;
根据不等式的几何性质,所以对于 的充要条件是
的充要条件是 表示点x到1和a两点的距离之和。 ∴f(x)的最小值为|a-1| ,所以对于
表示点x到1和a两点的距离之和。 ∴f(x)的最小值为|a-1| ,所以对于 的充要条件是|a-1|≥2 ,解得a≥3或a≤-1.
的充要条件是|a-1|≥2 ,解得a≥3或a≤-1.
考点:本题考查绝对值不等式,恒成立的问题
点评:解决本题的关键是熟练掌握绝对值的几何意义和不等式的几何性质

练习册系列答案
相关题目
 ,
, ,
, ,则
,则 B.
B. C.
C. D.
D.


 B.
B.
 C.
C.
 D.
D.

 ”是“
”是“ ”( )条件
”( )条件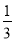 ,某植物研究所进行该种子的发芽实验,每次实验种一粒种子,每次实验结果相互独立,假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败.若该研究所共进行四次实验,设ξ表示四次实验结束时实验成功的次数与失败的次数之差的绝对值.
,某植物研究所进行该种子的发芽实验,每次实验种一粒种子,每次实验结果相互独立,假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败.若该研究所共进行四次实验,设ξ表示四次实验结束时实验成功的次数与失败的次数之差的绝对值.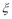 x-1在区间(2,3)上有且只有一个零点”为事件A,求事件A发生的概率P(A).
x-1在区间(2,3)上有且只有一个零点”为事件A,求事件A发生的概率P(A).
 对任意
对任意 恒成立,则实数x的取值范围是( )
恒成立,则实数x的取值范围是( )  B.
B.
 D.
D.


 为第三象限角,
为第三象限角, ,
, ;
; ,求
,求