题目内容
20.已知点A,B,C,D均在球O上,AB=BC=$\sqrt{3}$,AC=3,若三棱锥D-ABC体积的最大值为$\frac{3\sqrt{3}}{4}$,则球O的表面积为16π.分析 确定S△ABC=$\frac{3\sqrt{3}}{4}$,△ABC的外接圆的半径为$\sqrt{3}$,利用三棱锥D-ABC的体积的最大值为$\frac{3\sqrt{3}}{4}$,可得D到平面ABC的最大距离为1,再利用射影定理,即可求出球的半径,即可求出球O的表面积.
解答 解:∵AB=BC=$\sqrt{3}$,AC=3,
∴S△ABC=$\frac{1}{2}$×3×$\sqrt{3-\frac{9}{4}}$=$\frac{3\sqrt{3}}{4}$,
∵三棱锥D-ABC的体积的最大值为$\frac{3\sqrt{3}}{4}$,
∴D到平面ABC的最大距离为1,
∵cos∠A=$\frac{\sqrt{3}}{2}$,
∴sin∠A=$\frac{1}{2}$,
设△ABC的外接圆的半径为r,则2r=2$\sqrt{3}$,∴r=$\sqrt{3}$;
设球的半径为R,则($\sqrt{3}$)2=1×(2R-1),
∴R=2,
∴球O的表面积为4πR2=16π.
故答案为:16π.
点评 本题考查球的半径,考查体积的计算,确定D到平面ABC的最大距离为1是关键.

练习册系列答案
相关题目
7.下列表示同一个函数的是( )
| A. | y=lnex与y=elnx | B. | $y={t^{\frac{1}{2}}}$与$y={t^{\frac{2}{4}}}$ | ||
| C. | y=x0与y=$\frac{1}{x^0}$ | D. | $y=cos(t+\frac{π}{2})$与y=sint |
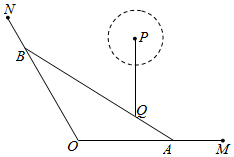 如图,A、B是海岸线OM、ON上的两个码头,Q为海中一小岛,在水上旅游线AB上,测得tan∠MON=-3,OA=6km,Q到海岸线OM、ON的距离分别为2km,$\frac{7\sqrt{10}}{5}$km.
如图,A、B是海岸线OM、ON上的两个码头,Q为海中一小岛,在水上旅游线AB上,测得tan∠MON=-3,OA=6km,Q到海岸线OM、ON的距离分别为2km,$\frac{7\sqrt{10}}{5}$km.