题目内容
12.求函数y=$\frac{sinx}{2+cosx}$的最大值.分析 变形可得y=$\frac{sinx}{2+cosx}$=$\frac{sinx-0}{cosx-(-2)}$表示点(cosx,sinx)和A(-2,0)连线的斜率,由直线和圆的知识可得.
解答 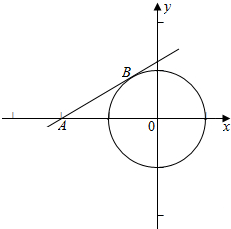 解:y=$\frac{sinx}{2+cosx}$=$\frac{sinx-0}{cosx-(-2)}$,表示点(cosx,sinx)和A(-2,0)连线的斜率,
解:y=$\frac{sinx}{2+cosx}$=$\frac{sinx-0}{cosx-(-2)}$,表示点(cosx,sinx)和A(-2,0)连线的斜率,
而由cos2x+sin2x=1可知点(cosx,sinx)在单位圆x2+y2=1上,
数形结合可得在图中切线AB时,y取最大值,
由三角形的知识可得∠BAO=30°,
故y取最大值tan30°=$\frac{\sqrt{3}}{3}$.
点评 本题考查三角函数的最值,数形结合是解决问题的关键,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.直线a与平面α所成的角为50°,直线b∥α,则b与α所成的角等于( )
| A. | 40° | B. | 50° | C. | 90° | D. | 150° |
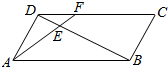 如图,点E是平行四边形ABCD对角线BD的n(n∈N且n≥2)等分点中最靠近点D的那点.线段AE的延长线交CD于点F,若向量$\overrightarrow{AF}=\frac{1}{n-1}\overrightarrow{AB}+x\overrightarrow{AD}$,则实数x的值为1.
如图,点E是平行四边形ABCD对角线BD的n(n∈N且n≥2)等分点中最靠近点D的那点.线段AE的延长线交CD于点F,若向量$\overrightarrow{AF}=\frac{1}{n-1}\overrightarrow{AB}+x\overrightarrow{AD}$,则实数x的值为1.