题目内容
14.[x]表示不超过x的最大整数,如[0.9]=0,[2.6]=2,则[lg1]+[lg2]+[lg3]+…+[lg100]=92.分析 由于[lg1]=[lg2]=[lg3]=…[lg9]=0,[lg10]=[lg11]=…+[lg99]=1,[lg100]=2.即可得出.
解答 解:∵[lg1]=[lg2]=[lg3]=…[lg9]=0,
[lg10]=[lg11]=…+[lg99]=1,
[lg100]=2.
∴[lg1]+[lg2]+[lg3]+…+[lg100]=90×1+2=92.
故答案为:92.
点评 本题考查了新定义、对数的运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.已知等差数列{an}的前9项和等于99,a10=21,则a20=( )
| A. | 31 | B. | 41 | C. | 51 | D. | 61 |
9.下列各数中,最小的数是( )
| A. | 75 | B. | 11111(2) | C. | 210(6) | D. | 85(9) |
4.已知函数f(x)=$\left\{\begin{array}{l}{(a-2)x,x≥2}\\{(\frac{1}{2})^{x}-1,x<2}\end{array}\right.$,满足对任意的实数x1≠x2,都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0成立,则实数a的取值范围为( )
| A. | (-∞,2) | B. | [$\frac{13}{4}$,2) | C. | [$\frac{13}{8}$,2) | D. | (-∞,$\frac{13}{8}$] |
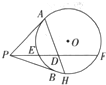 如图,已知点P是圆O外一点,过P做圆O的切线PA,PB,切点分别为A,B,过P做一条割线交圆O于E,F,若2PA=PF,取PF的中点D,连接AD,并延长交圆于H.
如图,已知点P是圆O外一点,过P做圆O的切线PA,PB,切点分别为A,B,过P做一条割线交圆O于E,F,若2PA=PF,取PF的中点D,连接AD,并延长交圆于H.