题目内容
已知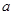 是实数,函数
是实数,函数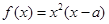 。
。
(Ⅰ)若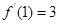 ,求
,求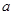 的值及曲线
的值及曲线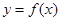 在点
在点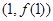 处的切线方程;
处的切线方程;
(Ⅱ)求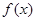 在区间
在区间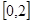 上的最大值。
上的最大值。
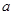 是实数,函数
是实数,函数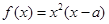 。
。(Ⅰ)若
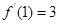 ,求
,求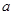 的值及曲线
的值及曲线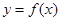 在点
在点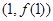 处的切线方程;
处的切线方程;(Ⅱ)求
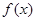 在区间
在区间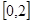 上的最大值。
上的最大值。(1) (2)
(2)
 (2)
(2)
试题分析:(Ⅰ)解:
 ,
,因为
 ,
,所以
 .
.又当
 时,
时, ,
, ,
,所以曲线
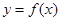 在
在 处的切线方程为
处的切线方程为 .
.(Ⅱ)解:令
 ,解得
,解得 ,
, .
.当
 ,即
,即 时,
时,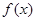 在
在 上单调递增,从而
上单调递增,从而 .
.当
 ,即
,即 时,
时,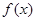 在
在 上单调递减,从而
上单调递减,从而 .
.当
 ,即
,即 时,
时,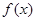 在
在 上单调递减,在
上单调递减,在 上单调递增,从而
上单调递增,从而
综上所述,

点评:该试题属于常规试题,解题的时候只要审题清晰,表示为数学代数式即可,让那后金额和函数求解最值。属于基础题。

练习册系列答案
相关题目
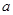 为常数,已知函数
为常数,已知函数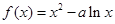 在区间
在区间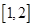 上是增函数,
上是增函数,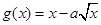 在区间
在区间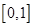 上是减函数.
上是减函数.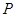 为函数
为函数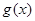 的图像上任意一点,求点
的图像上任意一点,求点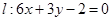 的距离的最小值;
的距离的最小值;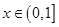 且
且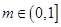 ,
,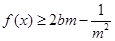 恒成立,求实数
恒成立,求实数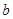 的取值范围.
的取值范围.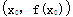 为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心;且“拐点”就是对称中心.”请你根据这一发现,请回答问题:
为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心;且“拐点”就是对称中心.”请你根据这一发现,请回答问题: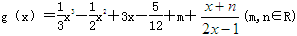 ,
,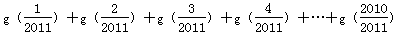 = .
= .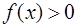 ,则当
,则当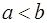 时,定积分
时,定积分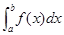 的符号( )
的符号( )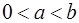 时是正的,当
时是正的,当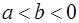 时是负的
时是负的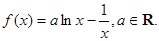
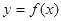 在点
在点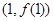 处的切线与直线
处的切线与直线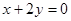 垂直,求a的值;
垂直,求a的值;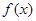 的单调区间;
的单调区间;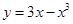 上切点为
上切点为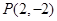 的切线方程是( )
的切线方程是( )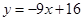
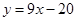
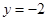
 处的导数
处的导数 的几何意义是
的几何意义是 处的斜率
处的斜率 处的切线与
处的切线与 轴所夹锐角的正切值
轴所夹锐角的正切值 在点
在点 在
在 处的切线与直线ax+2y+1=0互相垂直,则实数a的值等于( )
处的切线与直线ax+2y+1=0互相垂直,则实数a的值等于( )