题目内容
4.若函数f(x)=$\left\{\begin{array}{l}{-x+6,x≤2}\\{3+lo{g}_{2}x,x>2}\end{array}\right.$的值域为[4,+∞).分析 根据一次函数和对数函数的单调性,可以分别判断x≤2和x>2时f(x)的单调性,根据单调性便可得出f(x)的范围,从而便可得出函数f(x)的值域.
解答 解:①x≤2时,f(x)=-x+6为减函数;
∴f(x)≥f(2)=4;
②x>2时,f(x)=3+log2x为增函数;
∴f(x)>f(2)=4;
∴综上得,f(x)的值域为[4,+∞);
故答案为:[4,+∞).
点评 考查函数值域的概念,分段函数值域的求法,一次函数和对数函数的单调性,函数单调性的定义,根据单调性定义求函数值域的方法.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
16.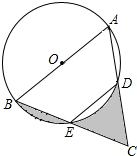 如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )
如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )
 如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )
如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
13.以模型y=cekx去拟合一组数据时,为了求出回归方程,设z=lny,其变换后得到线性回归方程z=0.3x+4,则c=( )
| A. | 0.3 | B. | e0.3 | C. | 4 | D. | e4 |
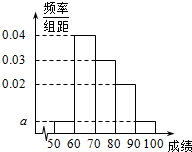 某校200位学生期末考试物理成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
某校200位学生期末考试物理成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].