题目内容
(本小题满分12分)
已知等差数列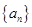 满足:
满足: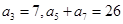 .
.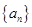 的前
的前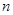 项和为
项和为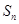 。
。
(Ⅰ)求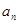 及
及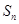 ;
;
(Ⅱ)令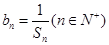 ,求数列
,求数列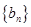 的前
的前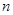 项和
项和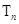 并证明
并证明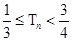 .
.
解析试题分析:(I)因为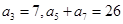 ,由等差数列的性质得
,由等差数列的性质得 ,所以
,所以 =13,d=
=13,d= =2,
=2, =3,
=3, ,
,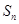 =
=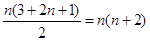 ;
;
(II)由(I) ,所以
,所以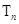 =
=
= (1+
(1+ -
- -
-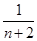 )=
)= -
- <
< ,
,
因为n=1时,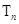 =
=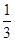 最小,所以
最小,所以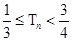 。
。
考点:本题主要考查等差数列的性质,求和公式,“裂项相消法”求和,“放缩法”证明不等式。
点评:中档题,本题具有一定的综合性,本解答从确定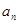 入手,进一步认识数列
入手,进一步认识数列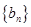 的特征,利用“裂项相消法”达到求
的特征,利用“裂项相消法”达到求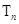 的目的,最后通过放缩实现不等式证明。“分组求和法”“错位相减法”也是常常考到的求和方法。
的目的,最后通过放缩实现不等式证明。“分组求和法”“错位相减法”也是常常考到的求和方法。

练习册系列答案
相关题目
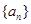 的前
的前 项和
项和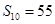 ,且
,且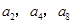 成等比数列.
成等比数列.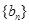 满足
满足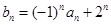 ,求
,求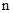 项和
项和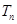 .
.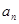 }中,
}中, ,
, ,且满足
,且满足
 ,求
,求 .
. 是有穷等差数列,给出下面数表:
是有穷等差数列,给出下面数表:

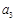 ……
…… 
 第1行
第1行
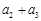 ……
…… 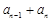 第2行
第2行 ,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为
,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为 .
. ,求和
,求和 .
. ,且
,且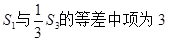
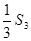 , 求和Tn=a1b1+a2b2+…+anbn
, 求和Tn=a1b1+a2b2+…+anbn 的前
的前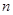 项和为
项和为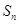 ,且
,且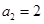 ,
,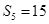 ,数列
,数列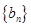 满足:
满足: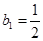 ,
, ,
,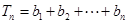 ,
,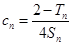 ,证明:
,证明:
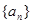 的前n项和为
的前n项和为 ,且
,且 ,(
,( =1,2,3…)
=1,2,3…)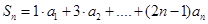 ,求
,求 为等差数列,且
为等差数列,且 ,
, .
. ,求证:数列
,求证:数列 是等比数列.
是等比数列.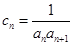 ,求数列
,求数列 的前
的前 项和
项和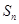 .
. 的前项和为
的前项和为 ,且
,且 ,
, 为等差数列,且
为等差数列,且 ,
, .
. ,求数列
,求数列 的前
的前 项和
项和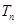 .
.