题目内容
设F1、F2是椭圆E: 的左、右焦点,P为直线
的左、右焦点,P为直线 上一点,
上一点,
△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
A. | B. | C. | D. |
C
解析试题分析:根据题意,由于F1、F2是椭圆E: 的左、右焦点,P为直线
的左、右焦点,P为直线 上一点,那么结合△F2PF1是底角为30°的等腰三角形,F2F1=F2P="2c,"
上一点,那么结合△F2PF1是底角为30°的等腰三角形,F2F1=F2P="2c,"  ,故可知答案为C.
,故可知答案为C.
考点:椭圆的性质
点评:主要是考查了椭圆的方程和性质的运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
抛物线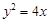 的焦点为
的焦点为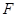 ,点
,点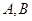 在抛物线上,且
在抛物线上,且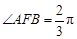 ,弦
,弦 中点
中点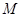 在准线
在准线 上的射影为
上的射影为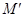 ,则
,则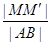 的最大值为( )
的最大值为( )
A.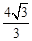 | B.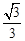 | C.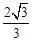 | D.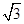 |
已知双曲线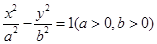 ,两渐近线的夹角为
,两渐近线的夹角为 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A.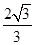 | B.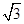 | C. | D.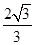 或 或 |
点 到图形
到图形 上每一个点的距离的最小值称为点
上每一个点的距离的最小值称为点 到图形
到图形 的距离,那么平面内到定圆
的距离,那么平面内到定圆 的距离与到定点
的距离与到定点 的距离相等的点的轨迹不可能是( )
的距离相等的点的轨迹不可能是( )
| A.圆 | B.椭圆 | C.双曲线的一支 | D.直线 |
已知双曲线 的两条渐近线均与
的两条渐近线均与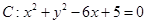 相切,则该双曲线离心率等于
相切,则该双曲线离心率等于
A.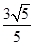 | B.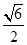 | C.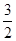 | D.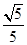 |
抛物线 上的一动点
上的一动点 到直线
到直线 距离的最小值是 ( )
距离的最小值是 ( )
A. | B. | C. | D. |
将两个顶点在抛物线 上,另一个顶点
上,另一个顶点 ,这样的正三角形有( )
,这样的正三角形有( )
| A.0个 | B.2个 | C.4个 | D.1个 |
极坐标方程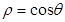 和参数方程
和参数方程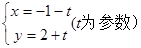 所表示的图形分别是( )
所表示的图形分别是( )
| A.直线,直线 | B.直线,圆 |
| C.圆,圆 | D.圆,直线 |
双曲线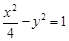 的顶点到渐进线的距离等于( )
的顶点到渐进线的距离等于( )
A.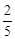 | B.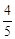 | C.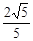 | D.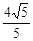 |