题目内容
对有 个元素的总体
个元素的总体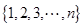 进行抽样,先将总体分成两个子总体
进行抽样,先将总体分成两个子总体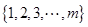 和
和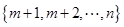 (
(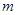 是给定的正整数,且
是给定的正整数,且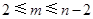 ),再从每个子总体中各随机抽取
),再从每个子总体中各随机抽取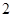 个元素组成样本.用
个元素组成样本.用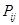 表示元素
表示元素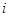 和
和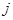 同时出现在样本中的概率.
同时出现在样本中的概率.
(1)求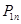 的表达式(用
的表达式(用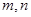 表示);
表示);
(2)求所有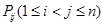 的和.
的和.
(1)  (2)
(2) 
解析试题分析:(1) 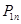 表示元素
表示元素 和
和 必取,
必取,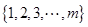 中再取一个,由
中再取一个,由 种取法,
种取法,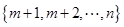 中再取一个,由
中再取一个,由 种取法,所以
种取法,所以 .(2)
.(2) 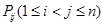 分三种情况,当
分三种情况,当 都在
都在 中时,
中时, ,而从
,而从 中选两个数的不同方法数为
中选两个数的不同方法数为 ,则
,则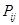 的和为
的和为 .当
.当 同时在
同时在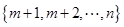 中时,同理可得
中时,同理可得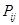 的和为
的和为 .当
.当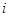 在
在 中,
中,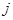 在
在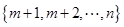 中时,
中时, ,而从
,而从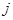
 中选取一个数,从
中选取一个数,从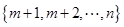 中选一个数的不同方法数为
中选一个数的不同方法数为 ,
,
则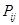 的和为
的和为 .所以所有
.所以所有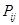 的和为
的和为 .
.
(1) .
.
(2)当 都在
都在 中时,
中时, ,
,
而从 中选两个数的不同方法数为
中选两个数的不同方法数为 ,则
,则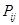 的和为
的和为 .
.
当 同时在
同时在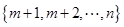 中时,同理可得
中时,同理可得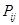 的和为
的和为 .
.
当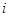 在
在 中,在
中,在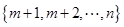 中时,
中时, ,
,
而从 中选取一个数,从
中选取一个数,从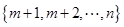 中选一个数的不同方法数为
中选一个数的不同方法数为 ,
,
则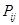 的和为
的和为 .所以所有
.所以所有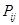 的和为
的和为 .
.
考点:古典概型概率

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
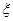 ,求
,求 .
.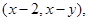 记
记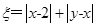 .
.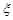 的最大值,并求事件“
的最大值,并求事件“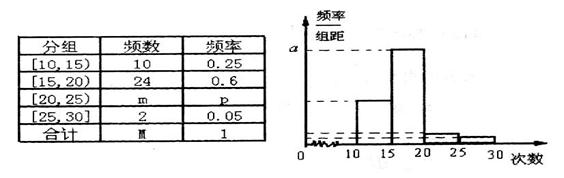
 .
. 内任取一个实数
内任取一个实数 ,设事件
,设事件 ={函数
={函数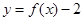 在区间
在区间 上有两个不同的零点},求事件
上有两个不同的零点},求事件 )得到的点数分别为
)得到的点数分别为 ,记事件
,记事件 {
{ 在
在 恒成立},求事件
恒成立},求事件 发生的概率.
发生的概率.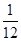 (i=1,2,…,12);设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大?
(i=1,2,…,12);设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大? 三个社区参加社会实践,要求每个社区至少有一名同学.
三个社区参加社会实践,要求每个社区至少有一名同学. 社区的概率;
社区的概率; 为四名同学中到
为四名同学中到 的值.
的值.