题目内容
对实验中学高三年级学生参加社区服务次数进行统计,随机抽取M名学生作样本,得到这M名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图: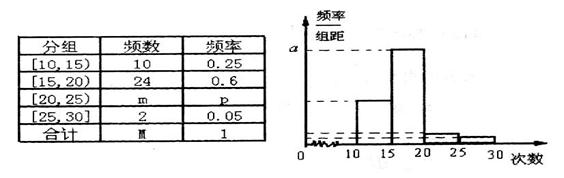
(1)求出表中M,p及图中a的值;
(2)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求两人来自同一小组的概率.
(1)M=40,p=0.1,a=0.12;(2)两人来自同一小组的概率为 .
.
解析试题分析:(1)由频率和为1求出p,再根据比例可求表中M及图中a的值;
(2)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人共15种可能,两人来自同一小组有7种可能,所以概率为 .
.
(1)由分组知 内的频数为10,频率为0.25,所以
内的频数为10,频率为0.25,所以 ,M=40.........1分
,M=40.........1分
P=1-0.25-0.6-0.05=0.1...........2分  ...........3分
...........3分
2)m=40-10-24-2=4,社区服务的次数不少于20次的学生共有m+2=6............4分 ,设为
,设为 ,
, 小组有2人,设为
小组有2人,设为 ,则任选2人,
,则任选2人,
共有15种: .................6分
.................6分
来自于同一组的有7种: ............8分
............8分
在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求两人来自同一小组的概率.P= ..................9分
..................9分
考点:频率与概率.

 期末集结号系列答案
期末集结号系列答案某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生.
(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.
甲的频数统计表(部分)
| 运行次数n | 输出y的值 为1的频数 | 输出y的值 为2的频数 | 输出y的值 为3的频数 |
| 30 | 14 | 6 | 10 |
| … | … | … | … |
| 2 100 | 1 027 | 376 | 697 |
乙的频数统计表(部分)
| 运行次数n | 输出y的值 为1的频数 | 输出y的值 为2的频数 | 输出y的值 为3的频数 |
| 30 | 12 | 11 | 7 |
| … | … | … | … |
| 2 100 | 1 051 | 696 | 353 |
当n=2 100时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编程序符合算法要求的可能性较大;
(3)将按程序框图正确编写的程序运行3次,求输出y的值为2的次数ξ的分布列及数学期望.
根据以往的经验,某工程施工期间的降水量X(单位:mm)对工期的影响如下表:
| 降水量X | 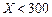 | 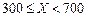 | 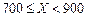 | 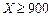 |
工期延误天数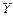 | 0 | 2 | 6 | 10 |
(1)工期延误天数
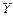 的均值与方差;(2)在降水量X至少是300的条件下,工期延误不超过6天的概率.
的均值与方差;(2)在降水量X至少是300的条件下,工期延误不超过6天的概率. 对有 个元素的总体
个元素的总体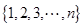 进行抽样,先将总体分成两个子总体
进行抽样,先将总体分成两个子总体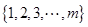 和
和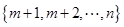 (
(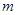 是给定的正整数,且
是给定的正整数,且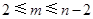 ),再从每个子总体中各随机抽取
),再从每个子总体中各随机抽取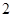 个元素组成样本.用
个元素组成样本.用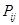 表示元素
表示元素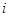 和
和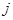 同时出现在样本中的概率.
同时出现在样本中的概率.
(1)求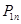 的表达式(用
的表达式(用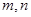 表示);
表示);
(2)求所有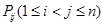 的和.
的和.
某商店试销某种商品20天,获得如下数据:
| 日销售量(件) | 0 | 1 | 2 | 3 |
| 频数 | 1 | 5 | 9 | 5 |
(1)求当天商店不进货的概率;
(2)记X为第二天开始营业时该商品视为件数,求X的分布列和数学期望.
 各人是否需使用设备相互独立.
各人是否需使用设备相互独立.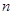 个黑球(
个黑球(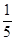 ,求
,求 ,V(η)=
,V(η)= ,求a∶b∶c.
,求a∶b∶c.