题目内容
 如图,在?OABP中,过点P的直线与线段OA、OB分别交与点M、N,若
如图,在?OABP中,过点P的直线与线段OA、OB分别交与点M、N,若| OM |
| OA |
| ON |
| OB |
(1)求函数y=f(x)的解析式;
(2)讨论f(x)的单调性,并求f(x)的值域.
分析:(1)应充分利用平面向量的基本定理,找准基底将向量
、
分别利用基底表示,再结合向量的共线即可获得问题的解答.
(2)结合反比例函数的单调性,及函数图象的平移变换法则,可分析出f(x)的单调性,进而求出f(x)的值域
| OA |
| OB |
(2)结合反比例函数的单调性,及函数图象的平移变换法则,可分析出f(x)的单调性,进而求出f(x)的值域
解答:解:(1)∵P,M,N三点共线,
=x•
,
=y•
.
则
=λ
+(1-λ)
=λx•
+(1-λ)(
-
),
∴y•
=(1-λ)
+(λx-1+λ)•
∴y=1-λ,λx-1+λ=0
∴y=1-
=
(x≥0)
(2)∵y=
在(0,+∞)上为增函数
∴y=
在[0,+∞)上为增函数
∴y=1-
在[0,+∞)上为增函数
∴y∈[0,1)
故函数求f(x)的值域为[0,1)
| OM |
| OA |
| ON |
| OB |
则
| ON |
| OM |
| OP |
| OA |
| OB |
| OA |
∴y•
| OB |
| OB |
| OA |
∴y=1-λ,λx-1+λ=0
∴y=1-
| 1 |
| 1+x |
| x |
| 1+x |
(2)∵y=
| -1 |
| x |
∴y=
| -1 |
| x+1 |
∴y=1-
| 1 |
| 1+x |
∴y∈[0,1)
故函数求f(x)的值域为[0,1)
点评:本题考查的知识点是平面向量的应用,其中三点共线的充要条件即P,M,N三点共线时
=λ
+(1-λ)
是解答本题的关键.
| ON |
| OM |
| OP |

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 如图,在平行四边形OABP中,过点P的直线与线段OA、OB分别相交于点M、N,若
如图,在平行四边形OABP中,过点P的直线与线段OA、OB分别相交于点M、N,若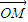 =x
=x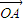 ,
,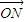 =y
=y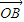
 +x,判断F(x)的单调性,并给出你的证明.
+x,判断F(x)的单调性,并给出你的证明.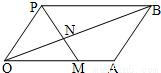
 =x•
=x• ,
, =y•
=y• .
.
 =x•
=x• ,
, =y•
=y• .
.