题目内容
如图，在平行四边形OABP中，过点P的直线与线段OA、OB分别相交于点M、N，若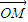
=x
，
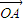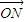=y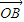
（0＜x＜1）．
（1）求y=f（x）的解析式；
（2）令F（x）=
+x，判断F（x）的单调性，并给出你的证明．
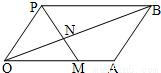
【答案】分析：（1）应充分利用平面向量的基本定理，找准基底将向量
分别利用基底表示，再结合向量的共线即可获得问题的解答．
（2）首先利用（1）的结论将F（x） 进行化简，然后利用函数单调性的定义即可获得问题的解答．
解答：解：（1）
=
=
-
，
则
=
-
=x
-y
，
=
-
=（
-
）-x
=-（1+x）
+
又
∥
，有x-y（1+x）=0，
即函数的解析式为：f（x）=
（0＜x＜1）；
（2）由（1）得F（x）=
+x=
+x=x+
+1（0＜x＜1），设0＜x1＜x2＜1，
则F（x1）-F（x2）=（x1+
+1）-（x2+
+1）=（x1-x2）+（
-
）
=（x1-x2）（1-
）=（x1-x2）
，
由0＜x1＜x2＜1，得x1-x2＜0，x1x2-1＜0，x1x2＞0，得F（x1）-F（x2）＞0，
即F（x1）＞F（x2）．
∴F（x）在（0，1）上为减函数．
点评：本题考查的是平面向量和函数性质的综合类问题．在解答的过程当中充分体现了平面向量的基本定理、共线知识以及函数单调性的定义．值得同学们体会和反思．
分别利用基底表示，再结合向量的共线即可获得问题的解答．（2）首先利用（1）的结论将F（x） 进行化简，然后利用函数单调性的定义即可获得问题的解答．
解答：解：（1）
==-，则
=-=x-y，=-=（-）-x=-（1+x）+又
∥，有x-y（1+x）=0，即函数的解析式为：f（x）=
（0＜x＜1）；（2）由（1）得F（x）=
+x=+x=x++1（0＜x＜1），设0＜x1＜x2＜1，则F（x1）-F（x2）=（x1+
+1）-（x2++1）=（x1-x2）+（-）=（x1-x2）（1-
）=（x1-x2），由0＜x1＜x2＜1，得x1-x2＜0，x1x2-1＜0，x1x2＞0，得F（x1）-F（x2）＞0，
即F（x1）＞F（x2）．
∴F（x）在（0，1）上为减函数．
点评：本题考查的是平面向量和函数性质的综合类问题．在解答的过程当中充分体现了平面向量的基本定理、共线知识以及函数单调性的定义．值得同学们体会和反思．
练习册系列答案
口算能手系列答案
相关题目
如图，在平行四边形OABC中，点O是原点，点A和点C的坐标分别是（3，0）、（1，3），点D是线段AB上的动点．
如图，在平行四边形OABC中，点O是原点，点A和点C的坐标分别是（3，0）、（1，3），点D是线段AB上的中点．
如图，在平行四边形ABCD中，O是对角线AC，BD的交点，N是线段OD的中点，AN的延长线与CD交于点E，则下列说法错误的是（ ）
（2009•浦东新区一模）如图，在平行四边形ABCD中，O为对角线交点，AB=2，AD=3，则
如图，在平行四边形OABC中，点O是原点，点A和点C的坐标分别是（3，0）、（1，3），点D是线段AB上的动点．