题目内容
如图所示，有一块半径为R的半圆形钢板，计划剪裁成等腰梯形ABCD的形状，它的下底AB是⊙O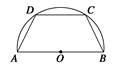
的直径,且上底CD的端点在圆周上，写出梯形周长y关于腰长x的函数关系式，并求出它的定义域.
的直径,且上底CD的端点在圆周上，写出梯形周长y关于腰长x的函数关系式，并求出它的定义域.
y=-
+2x+4R,定义域为（0，
R）
+2x+4R,定义域为（0，R）AB=2R，C、D在⊙o的半圆周上，
设腰长AD=BC=x，作DE⊥AB，
垂足为E，连接BD，
那么∠ADB是直角，
由此Rt△ADE∽Rt△ABD.
∴AD2=AE×AB，即AE=
，∴CD=AB-2AE=2R-，
所以y=2R+2x+（2R-
）,即y=-+2x+4R.
再由
,解得0＜x＜R.所以y=-+2x+4R,定义域为（0，R）.
设腰长AD=BC=x，作DE⊥AB，
垂足为E，连接BD，
那么∠ADB是直角，由此Rt△ADE∽Rt△ABD.
∴AD2=AE×AB，即AE=
，∴CD=AB-2AE=2R-，所以y=2R+2x+（2R-
）,即y=-+2x+4R.再由
,解得0＜x＜R.所以y=-+2x+4R,定义域为（0，R）.
练习册系列答案
相关题目
定义域是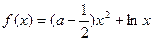 
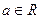
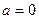时，求函数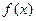
的单调递增区间；
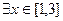，使
成立，求实数a的取值范围；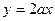
下方，求实数
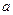的取值范围．
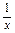);(3)y=f(
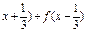; (4)y=f(x+a)+f(x-a).
在区间（0，2）内是否连续，在区间
上呢？
，求函数f(x)= 
的值域.
的定义域是 .
的定义域为
，值域为
，则
=________．
，则
