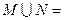题目内容
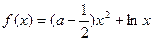
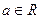
(1)当
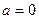 时,求函数
时,求函数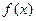 的单调递增区间;
的单调递增区间;(2)若
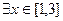 ,使
,使 成立,求实数a的取值范围;
成立,求实数a的取值范围;(3)若函数
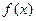 的图象在区间(1,+∞)内恒在直线
的图象在区间(1,+∞)内恒在直线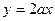 下方,求实数
下方,求实数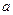 的取值范围.
的取值范围.(1)
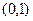 (2)
(2)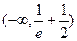 (3)
(3)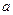 ∈[
∈[ ,
,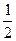 ]
]显然函数f(x)的定义域为 ………………1分
………………1分
(Ⅰ)当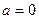 时,
时,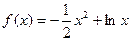 ,
,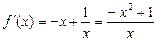 ;……………2分
;……………2分
由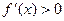 ,结合定义域解得
,结合定义域解得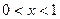 …………3分
…………3分
∴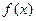 的单调递增区间为
的单调递增区间为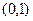 ,.……………………………4分
,.……………………………4分
(Ⅱ)将 化简得
化简得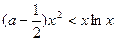 ,
,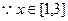 ∴有
∴有
令 ,则
,则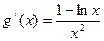 ,由
,由 解得
解得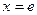 .…………6分
.…………6分
当 时,
时, ;当
;当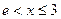 时,
时,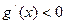
故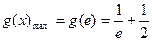
∴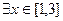 ,使
,使 成立等价于
成立等价于
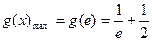
即a的取值范围为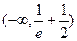 ……………………………8分
……………………………8分
(Ⅲ)令 ,则
,则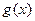 的定义域为(0,+∞).
的定义域为(0,+∞).
……………………………………………9分
在区间(1,+∞)上,函数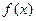 的图象恒在直线
的图象恒在直线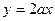 下方等价于
下方等价于
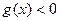 在区间(1,+∞)上恒成立.
在区间(1,+∞)上恒成立.
∵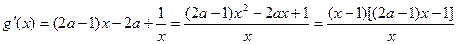
①若 ,令
,令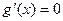 ,得极值点
,得极值点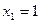 ,
,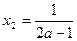 ,………………11分
,………………11分
当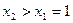 ,即
,即 时,在(
时,在( ,+∞)上有
,+∞)上有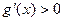 ,
,
此时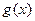 在区间(
在区间( ,+∞)上是增函数,并且在该区间上有
,+∞)上是增函数,并且在该区间上有
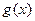 ∈(
∈(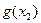 ,+∞),不合题意;………………………………………12分
,+∞),不合题意;………………………………………12分
当 ,即
,即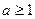 时,同理可知,
时,同理可知,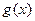 在区间(1,+∞)上,有
在区间(1,+∞)上,有
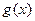 ∈(
∈( ,+∞),也不合题意;………………………………………13分
,+∞),也不合题意;………………………………………13分
②若 ,则有
,则有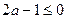 ,此时在区间(1,+∞)上恒有
,此时在区间(1,+∞)上恒有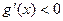 ,
,
从而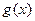 在区间(1,+∞)上是减函数;……………………………………14分
在区间(1,+∞)上是减函数;……………………………………14分
要使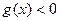 在此区间上恒成立,只须满足
在此区间上恒成立,只须满足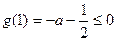
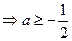 ,
,
由此求得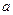 的范围是[
的范围是[ ,
,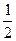 ].
].
综合①②可知,当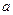 ∈[
∈[ ,
,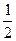 ]时,函数
]时,函数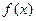 的图象恒在直线
的图象恒在直线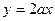 下方. 16分
下方. 16分
 ………………1分
………………1分(Ⅰ)当
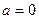 时,
时,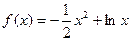 ,
,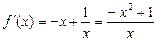 ;……………2分
;……………2分由
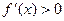 ,结合定义域解得
,结合定义域解得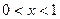 …………3分
…………3分∴
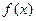 的单调递增区间为
的单调递增区间为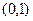 ,.……………………………4分
,.……………………………4分(Ⅱ)将
 化简得
化简得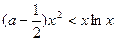 ,
,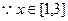 ∴有
∴有
令
 ,则
,则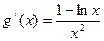 ,由
,由 解得
解得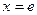 .…………6分
.…………6分当
 时,
时, ;当
;当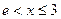 时,
时,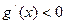
故
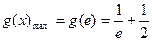
∴
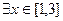 ,使
,使 成立等价于
成立等价于
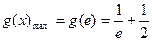
即a的取值范围为
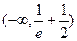 ……………………………8分
……………………………8分(Ⅲ)令
 ,则
,则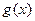 的定义域为(0,+∞).
的定义域为(0,+∞).……………………………………………9分
在区间(1,+∞)上,函数
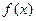 的图象恒在直线
的图象恒在直线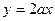 下方等价于
下方等价于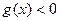 在区间(1,+∞)上恒成立.
在区间(1,+∞)上恒成立. ∵
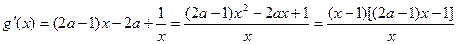
①若
 ,令
,令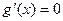 ,得极值点
,得极值点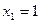 ,
,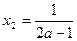 ,………………11分
,………………11分当
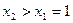 ,即
,即 时,在(
时,在( ,+∞)上有
,+∞)上有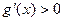 ,
,此时
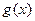 在区间(
在区间( ,+∞)上是增函数,并且在该区间上有
,+∞)上是增函数,并且在该区间上有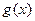 ∈(
∈(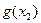 ,+∞),不合题意;………………………………………12分
,+∞),不合题意;………………………………………12分当
 ,即
,即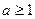 时,同理可知,
时,同理可知,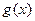 在区间(1,+∞)上,有
在区间(1,+∞)上,有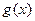 ∈(
∈( ,+∞),也不合题意;………………………………………13分
,+∞),也不合题意;………………………………………13分②若
 ,则有
,则有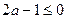 ,此时在区间(1,+∞)上恒有
,此时在区间(1,+∞)上恒有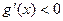 ,
,从而
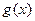 在区间(1,+∞)上是减函数;……………………………………14分
在区间(1,+∞)上是减函数;……………………………………14分要使
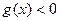 在此区间上恒成立,只须满足
在此区间上恒成立,只须满足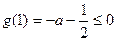
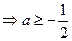 ,
,由此求得
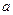 的范围是[
的范围是[ ,
,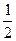 ].
].综合①②可知,当
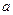 ∈[
∈[ ,
,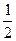 ]时,函数
]时,函数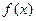 的图象恒在直线
的图象恒在直线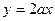 下方. 16分
下方. 16分
练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
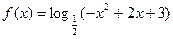
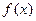 的定义域; (2)求
的定义域; (2)求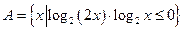
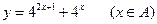 的值域
的值域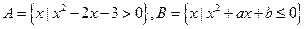 ,
,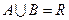 ,
,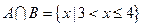 ,则
,则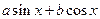 的最小值是多少?
的最小值是多少?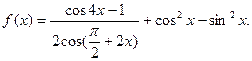
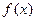 的定义域,值域。
的定义域,值域。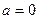 时,求
时,求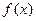 的极值;
的极值;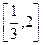 上是增函数,求实数
上是增函数,求实数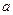 的取值范围
的取值范围
 函数
函数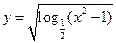 的定义域是( ).
的定义域是( ).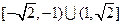
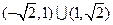
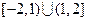
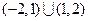
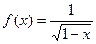 的定义域为
的定义域为 ,
,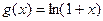 的定义域为
的定义域为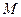 ,则
,则