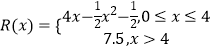题目内容
【题目】已知![]() .
.
(Ⅰ)若函数![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() ,证明:
,证明:![]() ,
,![]() 恒成立.
恒成立.
【答案】见解析
【解析】(Ⅰ)![]() .
.
由函数![]() 在
在![]() 上单调递增,可得
上单调递增,可得![]() 在
在![]() 上恒成立,
上恒成立,
即![]() ,得
,得![]() . -----------------2分
. -----------------2分
记![]() (
(![]() ),则
),则![]() .
.
当![]() 时,
时,![]() ,函数单调递减;当
,函数单调递减;当![]() 时,
时,![]() ,函数单调递增.
,函数单调递增.
所以![]() . -----------------5分
. -----------------5分
所以实数![]() 的取值范围为
的取值范围为![]() . ---------------------------6分
. ---------------------------6分
(Ⅱ)设![]() .
.
则![]() ,
,
记![]() ,则
,则![]() ,
,
故当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增. ------------9分
单调递增. ------------9分
又![]() ,
,![]() ,所以
,所以![]() ,使得
,使得![]() ,即
,即![]() .
.
所以当![]() 时,
时,![]() ,函数单调递增;
,函数单调递增;
当![]() 时,
时,![]() ,函数单调递减;
,函数单调递减;
当![]() 时,
时,![]() ,函数单调递增.
,函数单调递增.
而![]() ,
,
所以![]() 时,
时,![]() ,即
,即![]() 恒成立. -----------------13分
恒成立. -----------------13分
【命题意图】本题考查导数与函数的单调性、不等式的证明等,考查基本的逻辑推理能力、运算能力以及数学应用意识等.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目