Question

15．已知实数a，b，c满足${（\frac{1}{2}）^a}$=3，log₃b=-$\frac{1}{2}$，${（\frac{1}{3}）^c}={log_2}$c，则实数a，b，c的大小关系为（　　）

• A． a＜b＜c
• B． a＜c＜b
• C． c＜a＜b
• D． b＜c＜a

Answer 1

分析 分别化指数式为对数式与化对数式为指数式得到a，b的范围，再由指数函数与对数函数的图象可得c的范围，则实数a，b，c的大小关系可求．

解答 解：∵${（\frac{1}{2}）^a}$=3，∴a=$lo{g}_{\frac{1}{2}}3=-lo{g}_{2}3$＜0；
∵log₃b=-$\frac{1}{2}$，∴b=${3}^{-\frac{1}{2}}$=$\frac{\sqrt{3}}{3}$∈（0，1）；
由${（\frac{1}{3}）^c}={log_2}$c，作出指数函数与对数函数的图象如图：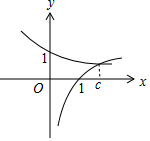

可知c＞1．
∴a＜b＜c．
故选：A．

点评 本题考查对数值的大小比较，考查指数函数与对数函数的图象，是中档题．