题目内容
已知函数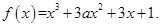
(I)当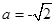 时,讨论
时,讨论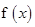 的单调性;
的单调性;
(II)若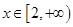 时,
时,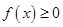 ,求
,求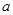 的取值范围.
的取值范围.
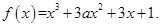
(I)当
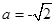 时,讨论
时,讨论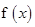 的单调性;
的单调性;(II)若
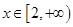 时,
时,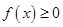 ,求
,求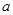 的取值范围.
的取值范围.(I)当 时,
时, ,
, 在
在 是增函数;
是增函数;
当 时,
时, ,
, 在
在 是减函数;
是减函数;
当 时,
时, ,
, 在
在 是增函数;
是增函数;
(II)
 时,
时, ,
, 在
在 是增函数;
是增函数;当
 时,
时, ,
, 在
在 是减函数;
是减函数;当
 时,
时, ,
, 在
在 是增函数;
是增函数;(II)

(Ⅰ)当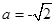 时,
时,
 .
.
令 ,得
,得 ,
, .
.
当 时,
时, ,
, 在
在 是增函数;
是增函数;
当 时,
时, ,
, 在
在 是减函数;
是减函数;
当 时,
时, ,
, 在
在 是增函数;
是增函数;
(Ⅱ)由 得
得 .
.
当 ,
, 时,
时,
 ,
,
所以 在
在 是增函数,于是当
是增函数,于是当 时,
时, .
.
综上,a的取值范围是 .
.
(1)直接利用求导的方法,通过导函数大于0和小于0求解函数单调区间;(2)解题关键是利用求导的方法和不等式的放缩进行证明 .
.
【考点定位】本题考查利用导数求解函数的单调性与参数范围问题.
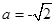 时,
时,
 .
.令
 ,得
,得 ,
, .
.当
 时,
时, ,
, 在
在 是增函数;
是增函数;当
 时,
时, ,
, 在
在 是减函数;
是减函数;当
 时,
时, ,
, 在
在 是增函数;
是增函数;(Ⅱ)由
 得
得 .
.当
 ,
, 时,
时, ,
,所以
 在
在 是增函数,于是当
是增函数,于是当 时,
时, .
.综上,a的取值范围是
 .
.(1)直接利用求导的方法,通过导函数大于0和小于0求解函数单调区间;(2)解题关键是利用求导的方法和不等式的放缩进行证明
 .
.【考点定位】本题考查利用导数求解函数的单调性与参数范围问题.

练习册系列答案
相关题目
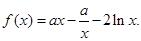
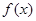 在
在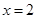 时有极值,求实数
时有极值,求实数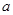 的值和
的值和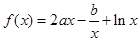 .
.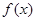 在
在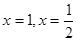 处取得极值,
处取得极值,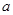 、
、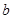 的值;②存在
的值;②存在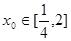 ,使得不等式
,使得不等式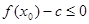 成立,求
成立,求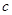 的最小值;
的最小值;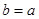 时,若
时,若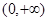 上是单调函数,求
上是单调函数,求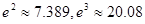 )
) 在
在 上是单调函数,则实数
上是单调函数,则实数 的取值范围是( )
的取值范围是( )



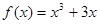 对任意的
对任意的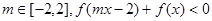 恒成立,则
恒成立,则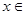 ___________.
___________.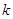 ,使得对定义域
,使得对定义域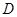 内的任意两个
内的任意两个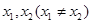 ,均有
,均有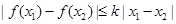 成立,则称函数
成立,则称函数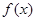 在定义域
在定义域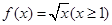 满足利普希茨条件,则常数
满足利普希茨条件,则常数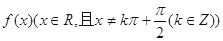 是周期为
是周期为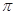 的函数,当x∈(
的函数,当x∈(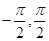 )时,
)时,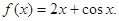 设
设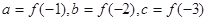 则
则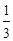 x3-
x3-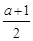 x2+a x.
x2+a x.
 时,求函数
时,求函数 的最值;
的最值;