题目内容
(本小题满分13分)
已知函数
(1) 当 时,求函数
时,求函数 的最值;
的最值;
(2) 求函数 的单调区间;
的单调区间;
已知函数

(1) 当
 时,求函数
时,求函数 的最值;
的最值;(2) 求函数
 的单调区间;
的单调区间;(1)函数f (x)的最小值为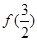 =
=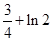 .
.
(2) a≤0时, f(x)的增区间为(1, +∞).
a>0时f(x)的减区间为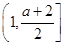 ,f(x)的增区间为
,f(x)的增区间为 .
.
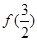 =
=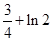 .
.(2) a≤0时, f(x)的增区间为(1, +∞).
a>0时f(x)的减区间为
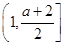 ,f(x)的增区间为
,f(x)的增区间为 .
. 试题分析:(1) 函数f(x)=x2-ax-aln(x-1)(a∈R)的定义域是(1,+∞) 1分
当a=1时,
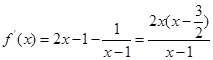 ,所以f (x)在
,所以f (x)在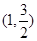 为减函数 3分
为减函数 3分在
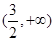 为增函数,所以函数f (x)的最小值为
为增函数,所以函数f (x)的最小值为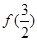 =
=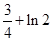 . 5分
. 5分(2)
 6分
6分若a≤0时,则
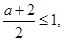 f(x)
f(x)
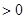 在(1,+∞)恒成立,所以f(x)的增区间为(1, +∞). 8分
在(1,+∞)恒成立,所以f(x)的增区间为(1, +∞). 8分若a>0,则
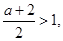 故当
故当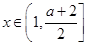 ,
,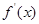

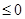 , 9分
, 9分当
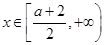 时,f(x)
时,f(x)
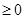 ,
,所以a>0时f(x)的减区间为
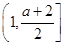 ,f(x)的增区间为
,f(x)的增区间为 . 13分
. 13分点评:典型题,本题属于导数应用中的基本问题,因为涉及到参数a,所以利用分类讨论的方法,研究a不同取值情况下,函数的单调性。涉及对数函数,要特别注意函数的定义域。

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
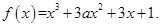
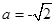 时,讨论
时,讨论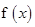 的单调性;
的单调性;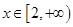 时,
时,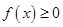 ,求
,求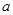 的取值范围.
的取值范围.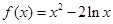 的单调递减区间为________.
的单调递减区间为________.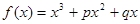 与
与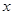 轴切于
轴切于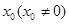 点,且极小值为
点,且极小值为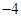 ,则
,则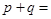 ( )
( )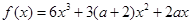 .
.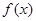 的两个极值点为
的两个极值点为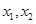 ,且
,且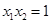 ,求实数
,求实数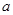 的值;
的值;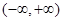 上的单调函数?若存在,求出
上的单调函数?若存在,求出 ,
, 是
是 的导函数(
的导函数( 为自然对数的底数)
为自然对数的底数) 的不等式:
的不等式: ;
; ,求实数
,求实数 的取值范围.
的取值范围.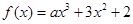 ,若
,若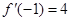 ,则
,则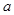 的值等于( )
的值等于( )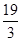


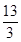
 .
. ,求
,求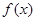 的最小值;
的最小值; ,讨论函数
,讨论函数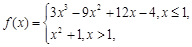 若
若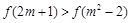 ,则实数
,则实数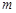 的取值范围是 .
的取值范围是 .