题目内容

10．从数字0、1、2、3、4、5这6个数字中任选三个不同的数字组成的三位偶数有52个．（用数字作答）

分析 分两类，第一类，个位为0，第二类，个位是2或4，再利用分步计数原理求出每一类有多少个，然后相加．

解答 解：分两类，第一类，个位为0，有A52=20个；
第二类，个位是2或4，有C21×C41×C41=32个，
∴可组成没有重复数字的三位偶数有20+32=52个，
故答案为：52．

点评 本题考查了分类、分步计数原理，考查了组合数公式，分类要不重不漏．

练习册系列答案
相关题目
7．已知f（x）=x+g（x），其中g（x）是定义在R上，最小正周期为2的函数．若f（x）在区间[2，4）上的最大值为1，则f（x）在区间[10，12）上的最大值为9．
18．如图，在正方体ABCD-A1B1C1D1中，若M是线段A1C1上的动点，则下列结论不正确的是（　　）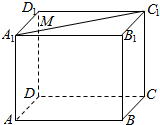
A．三棱锥M-ABD的主视图面积不变B．三棱锥M-ABD的侧视图面积不变
C．异面直线CM，BD所成的角恒为$\frac{π}{2}$D．异面直线CM，AB所成的角可为$\frac{π}{4}$
5．已知向量$\overrightarrow{α}$，$\overrightarrow{β}$是平面内两个互相垂直垂直的单位向量，若（5$\overrightarrow{α}$-2$\overrightarrow{γ}$）•（12$\overrightarrow{β}$-2$\overrightarrow{γ}$）=0，则|$\overrightarrow{γ}$|的最大值是$\frac{13}{2}$．
15．已知数列{an}为等差数列，数列{bn}满足bn=an+n，若b2，b5，b11成等比数列，且b3=a6．
（1）求an，bn；
（2）求数列{$\frac{1}{a_nb_n}$}的前n项和Sn．
2．下列四个命题：
①任意两条直线都可以确定一个平面；
②若两个平面有3个不同的公共点，则这两个平面重合；
③直线a，b，c，若a与b共面，b与c共面，则a与c共面；
④若直线l上有一点在平面α外，则l在平面α外．
其中错误命题的个数是（　　）
A．1B．2C．3D．4
19．已知函数f（x）是定义在（-∞，+∞）上的奇函数，若对于任意的实数x≥0，都有f（x+2）=f（x），且当x∈[0，2）时，f（x）=log2（x+1），则f（2014）+f（-2015）+f（2016）的值为（　　）
A．-1B．-2C．2D．1
20．如图，在△ABC中，AB=AC=3，cos∠BAC=$\frac{1}{3}$，$\overrightarrow{DC}$=2$\overrightarrow{BD}$，则$\overrightarrow{AD}$•$\overrightarrow{BC}$的值为-2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网