题目内容
在正三棱锥P-ABC(顶点在底面的射影是底面正三角形的中心)中,AB=4,PA=8,过A作与PB,PC分别交于D和E的截面,则截面△ADE的周长的最小值是 .
【答案】分析:画出正三棱锥P-ABC侧面展开图,将问题转化为求平面上两点间的距离最小值问题,不难求得结果.
解答: 解:三棱锥的侧面展开图,如图,
解:三棱锥的侧面展开图,如图,
△ADE的周长的最小值为AA1,
在△PAB中,sin ∠APB=
∠APB= ,∴cos∠APB=1-2sin2
,∴cos∠APB=1-2sin2 ∠APB=
∠APB= ,
,
在△APA1中,∴sin ∠APA1=sin(∠APB+
∠APA1=sin(∠APB+ ∠APB)=sin∠APBcos
∠APB)=sin∠APBcos ∠APB+cos∠APBsin
∠APB+cos∠APBsin ∠APB=
∠APB= +
+ ×
× =
= ,
,
所以AA1=2PA×sin ∠APA1=11,
∠APA1=11,
故答案为:11.
点评:本题考查的知识点是棱锥的结构特征,其中将三棱锥的侧面展开,将空间问题转化为平面上两点之间的距离问题,是解答本题的关键.
解答:
 解:三棱锥的侧面展开图,如图,
解:三棱锥的侧面展开图,如图,△ADE的周长的最小值为AA1,
在△PAB中,sin
 ∠APB=
∠APB= ,∴cos∠APB=1-2sin2
,∴cos∠APB=1-2sin2 ∠APB=
∠APB= ,
,在△APA1中,∴sin
 ∠APA1=sin(∠APB+
∠APA1=sin(∠APB+ ∠APB)=sin∠APBcos
∠APB)=sin∠APBcos ∠APB+cos∠APBsin
∠APB+cos∠APBsin ∠APB=
∠APB= +
+ ×
× =
= ,
,所以AA1=2PA×sin
 ∠APA1=11,
∠APA1=11,故答案为:11.
点评:本题考查的知识点是棱锥的结构特征,其中将三棱锥的侧面展开,将空间问题转化为平面上两点之间的距离问题,是解答本题的关键.

练习册系列答案
相关题目
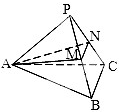 如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,底面边长为2,则此三棱锥的体积是( )
如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,底面边长为2,则此三棱锥的体积是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|