题目内容
已知函数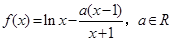 .
.
(1)若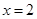 是函数
是函数 的极值点,求曲线
的极值点,求曲线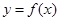 在点
在点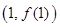 处的切线方程;
处的切线方程;
(2)若函数 在
在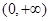 上为单调增函数,求
上为单调增函数,求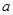 的取值范围.
的取值范围.
(1) ;(2)
;(2) .
.
解析试题分析:解题思路:(1)求导函数,利用 求
求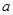 ;利用导数的几何意义求切线方程;(2)利用“若函数
;利用导数的几何意义求切线方程;(2)利用“若函数 在某区间上单调递增,则
在某区间上单调递增,则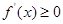 在该区间恒成立”求解.规律总结:(1)导数的几何意义求切线方程:
在该区间恒成立”求解.规律总结:(1)导数的几何意义求切线方程: ;(2)若函数
;(2)若函数 在某区间上单调递增,则
在某区间上单调递增,则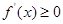 在该区间恒成立;“若函数
在该区间恒成立;“若函数 在某区间上单调递减,则
在某区间上单调递减,则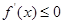 在该区间恒成立.
在该区间恒成立.
试题解析:(1)

由题意知 ,代入得
,代入得 ,经检验,符合题意.
,经检验,符合题意.
从而切线斜率
 ,切点为
,切点为 ,
,
切线方程为 .
.
(2)
因为 上为单调增函数,所以
上为单调增函数,所以 上恒成立.
上恒成立.
即 在
在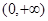 上恒成立;当
上恒成立;当 时,由
时,由 ,得
,得 ;设
;设 ,
, .
. .所以当且仅当
.所以当且仅当 ,即
,即 时,
时, 有最大值2.所以
有最大值2.所以 所以
所以 .
.
所以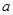 的取值范围是
的取值范围是
考点:1.导数的几何意义;2.根据函数的单调性求参数.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 .
. .
.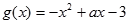 .
.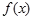 在区间
在区间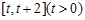 上的最小值;
上的最小值;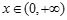 ,
,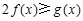 恒成立,求实数
恒成立,求实数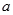 的取值范围;
的取值范围;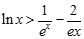 恒成立.
恒成立. ,对任意给定的正实数a,曲线y=F(x)上是否存在两点P,Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在y轴上?请说明理由.
,对任意给定的正实数a,曲线y=F(x)上是否存在两点P,Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在y轴上?请说明理由.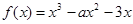 ,
,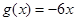 (
(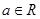 ).
).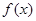 的极值点,求
的极值点,求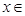 [1,a]上的最小值和最大值;
[1,a]上的最小值和最大值;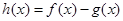 在
在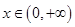 时是增函数,求实数a的取值范围.
时是增函数,求实数a的取值范围. ,
,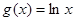 .
. 的极值;(2)若
的极值;(2)若 恒成立,求实数
恒成立,求实数 的值;
的值;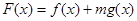
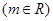 有两个极值点
有两个极值点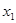 、
、 (
(
 的取值范围,并证明
的取值范围,并证明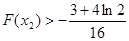 .
.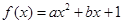 在
在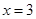 处的切线方程为
处的切线方程为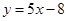 .
. 的解析式;
的解析式;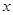 的方程
的方程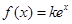 恰有两个不同的实根,求实数
恰有两个不同的实根,求实数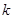 的值;
的值;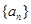 满足
满足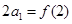 ,
,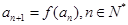 ,求
,求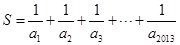 的整数部分.
的整数部分.
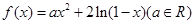 ,
,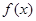 在
在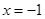 处有极值,求a;
处有极值,求a; 上为增函数,求a的取值范围.
上为增函数,求a的取值范围.