题目内容
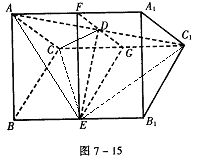
如图,在三棱锥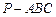 中,
中,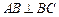 ,
,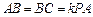 ,点
,点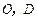 分别是
分别是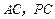 的中点,
的中点,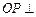 底面
底面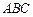 .
.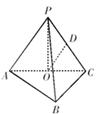
(1)求证: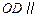 平面
平面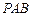 ;
;
(2)当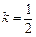 时,求直线
时,求直线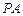 与平面
与平面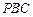 所成角的大小;
所成角的大小;
(3)当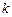 为何值时,
为何值时,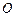 在平面
在平面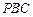 内的射影恰好为
内的射影恰好为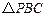 的重心?
的重心?
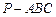 中,
中,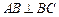 ,
,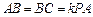 ,点
,点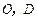 分别是
分别是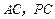 的中点,
的中点,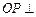 底面
底面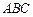 .
.
(1)求证:
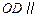 平面
平面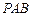 ;
;(2)当
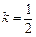 时,求直线
时,求直线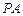 与平面
与平面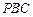 所成角的大小;
所成角的大小;(3)当
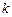 为何值时,
为何值时,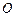 在平面
在平面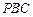 内的射影恰好为
内的射影恰好为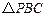 的重心?
的重心?(1)证明见解析(2)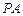 与平面
与平面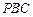 所成的角为
所成的角为 .(3)当
.(3)当 时,三棱锥
时,三棱锥 为正三棱锥.
为正三棱锥.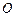 在平面
在平面 内的射影为
内的射影为 的重心.
的重心.
 与平面
与平面 所成的角为
所成的角为 .(3)当
.(3)当 时,三棱锥
时,三棱锥 为正三棱锥.
为正三棱锥.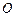 在平面
在平面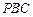 内的射影为
内的射影为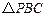 的重心.
的重心.(1)证明: 平面
平面 ,
,
 .
.
以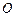 为原点,建立如图所示空间直角坐标系
为原点,建立如图所示空间直角坐标系 .
.

设 ,则
,则 .
.
设 ,则
,则 .
.
 为
为 的中点,
的中点, .
.
 ,
, .
.
 ,
, 平面
平面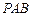 .
.
(2)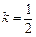 ,即
,即 ,
, ,
,

可求得平面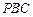 的法向量
的法向量 .
.
 .
.
设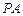 与平面
与平面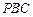 所成的角为
所成的角为 ,
,
则 .
.
 与平面
与平面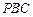 所成的角为
所成的角为 .
.
(3)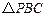 的重心
的重心 ,
, ,
,
 平面
平面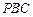 ,
, .
.
又 ,
, .
.
 .
.
 ,即
,即 .
.
反之,当 时,三棱锥
时,三棱锥 为正三棱锥.
为正三棱锥.
 在平面
在平面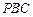 内的射影为
内的射影为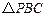 的重心.
的重心.
 平面
平面 ,
, .
.以
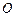 为原点,建立如图所示空间直角坐标系
为原点,建立如图所示空间直角坐标系 .
.
设
 ,则
,则 .
.设
 ,则
,则 .
. 为
为 的中点,
的中点, .
. ,
, .
. ,
, 平面
平面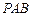 .
.(2)
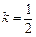 ,即
,即 ,
, ,
,
可求得平面
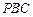 的法向量
的法向量 .
. .
.设
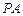 与平面
与平面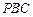 所成的角为
所成的角为 ,
,则
 .
. 与平面
与平面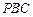 所成的角为
所成的角为 .
.(3)
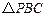 的重心
的重心 ,
, ,
, 平面
平面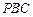 ,
, .
.又
 ,
, .
. .
. ,即
,即 .
.反之,当
 时,三棱锥
时,三棱锥 为正三棱锥.
为正三棱锥. 在平面
在平面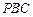 内的射影为
内的射影为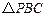 的重心.
的重心.
练习册系列答案
相关题目
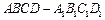 中,点
中,点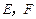 分别在
分别在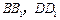 上,且
上,且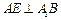 ,
,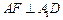 .
.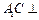 平面
平面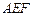 ;
;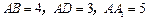 时,求平面
时,求平面 所成角的大小.
所成角的大小.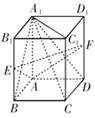
 中,
中, 分别为棱
分别为棱 的中点,已知
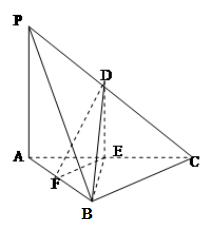
的中点,已知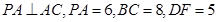 ,
,
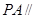 平面
平面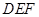 ;
;
 平面
平面 .
.
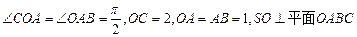 ,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.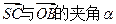 的大小(用反三角函数表示);
的大小(用反三角函数表示);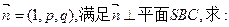
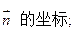
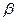 (用反三角函数表示);
(用反三角函数表示);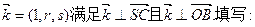
 .
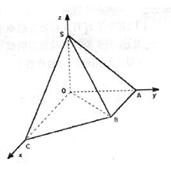
. 
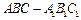 中,底面是等腰直角三角形,
中,底面是等腰直角三角形,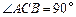 ,侧棱
,侧棱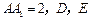 分别是
分别是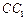 与
与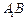 的中点,点
的中点,点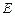 在平面
在平面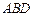 上的射影是
上的射影是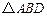 的重心
的重心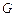 ,求点
,求点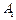 到平面
到平面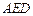 的距离.
的距离.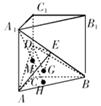
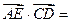 _ ▲ .
_ ▲ .