题目内容
设x2+y2=2的切线l与x轴的正半轴、y轴的正半轴分别交于点A、B,当|AB|取最小值时,切线l的方程为( )
分析:设出直线方程,由直线与圆相切,得到圆心到直线的距离等于圆的半径,化简可得a与b的关系式,利用此关系式把|AB|2进行变形,利用基本不等式求出|AB|2的最小值,且得到取最小值时a与b的值,把此时a与b的值代入所设的方程中,即可确定出切线的方程.
解答:解:设A(a,0),B(0,b),a>0,b>0,
则切线的方程为
+
=1
∵圆x2+y2=2的圆心坐标为(0,0),半径r=
,l与圆相切,
∴圆心到直线的距离d=
=
∴
=ab
∴ab≥4,当且仅当a=b时取等号
∴|AB|=
=
≥2
∴|AB|的最小值为2
,此时a=b=2,切线方程为x+y-2=0.
故选C.
则切线的方程为
| x |
| a |
| y |
| b |
∵圆x2+y2=2的圆心坐标为(0,0),半径r=
| 2 |
∴圆心到直线的距离d=
| |-ab| | ||
|
| 2 |
∴
| 2(a2+b2) |
∴ab≥4,当且仅当a=b时取等号
∴|AB|=
| a2+b2 |
| ab | ||
|
| 2 |
∴|AB|的最小值为2
| 2 |
故选C.
点评:本题考查圆的切线方程,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (a>b>0)的离心率与双曲线x2﹣y2=1的离心率互为倒数,且内切于圆x2+y2=4.
(a>b>0)的离心率与双曲线x2﹣y2=1的离心率互为倒数,且内切于圆x2+y2=4. x+m交椭圆于A、B两点,椭圆上一点
x+m交椭圆于A、B两点,椭圆上一点 ,求△PAB面积的最大值.
,求△PAB面积的最大值. (a>b>0)的离心率与双曲线x2-y2=1的离心率互为倒数,且内切于圆x2+y2=4.
(a>b>0)的离心率与双曲线x2-y2=1的离心率互为倒数,且内切于圆x2+y2=4. x+m交椭圆于A、B两点,椭圆上一点
x+m交椭圆于A、B两点,椭圆上一点 ,求△PAB面积的最大值.
,求△PAB面积的最大值. (a>b>0)的离心率与双曲线x2-y2=1的离心率互为倒数,且内切于圆x2+y2=4.
(a>b>0)的离心率与双曲线x2-y2=1的离心率互为倒数,且内切于圆x2+y2=4. x+m交椭圆于A、B两点,椭圆上一点
x+m交椭圆于A、B两点,椭圆上一点 ,求△PAB面积的最大值.
,求△PAB面积的最大值.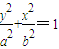 (a>b>0)的离心率与双曲线x2-y2=1的离心率互为倒数,且内切于圆x2+y2=4.
(a>b>0)的离心率与双曲线x2-y2=1的离心率互为倒数,且内切于圆x2+y2=4. x+m交椭圆于A、B两点,椭圆上一点
x+m交椭圆于A、B两点,椭圆上一点 ,求△PAB面积的最大值.
,求△PAB面积的最大值.