题目内容
设椭圆M: (a>b>0)的离心率与双曲线x2﹣y2=1的离心率互为倒数,且内切于圆x2+y2=4.
(a>b>0)的离心率与双曲线x2﹣y2=1的离心率互为倒数,且内切于圆x2+y2=4.
(1)求椭圆M的方程;
(2)若直线y= x+m交椭圆于A、B两点,椭圆上一点
x+m交椭圆于A、B两点,椭圆上一点 ,求△PAB面积的最大值.
,求△PAB面积的最大值.
 (a>b>0)的离心率与双曲线x2﹣y2=1的离心率互为倒数,且内切于圆x2+y2=4.
(a>b>0)的离心率与双曲线x2﹣y2=1的离心率互为倒数,且内切于圆x2+y2=4.(1)求椭圆M的方程;
(2)若直线y=
 x+m交椭圆于A、B两点,椭圆上一点
x+m交椭圆于A、B两点,椭圆上一点 ,求△PAB面积的最大值.
,求△PAB面积的最大值.解:(1)双曲线的离心率为 ,
,
则椭圆的离心率为
圆x2+y2=4的直径为4,则2a=4,
得:


所求椭圆M的方程为 .
.
(2)直线AB的直线方程: .
.
由 ,得
,得 ,
,
由 ,
,
得﹣2 <m<2
<m<2
∵ ,
, .
.
∴ =
=
又P到AB的距离为 .则
.则


当且仅当 取等号
取等号
∴ .
.
 ,
,则椭圆的离心率为

圆x2+y2=4的直径为4,则2a=4,
得:



所求椭圆M的方程为
 .
.(2)直线AB的直线方程:
 .
.由
 ,得
,得 ,
,由
 ,
,得﹣2
 <m<2
<m<2
∵
 ,
, .
.∴
 =
=
又P到AB的距离为
 .则
.则

当且仅当
 取等号
取等号∴
 .
. 
练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
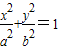 (a>b>0)的离心率为
(a>b>0)的离心率为 ,长轴长为
,长轴长为 ,设过右焦点F倾斜角为θ的直线交椭圆M于A,B两点.
,设过右焦点F倾斜角为θ的直线交椭圆M于A,B两点. ;
; (a>b>0)的离心率为
(a>b>0)的离心率为 ,长轴长为
,长轴长为 ,设过右焦点F倾斜角为θ的直线交椭圆M于A,B两点.
,设过右焦点F倾斜角为θ的直线交椭圆M于A,B两点. ;
; (a>b>0)的离心率与双曲线x2-y2=1的离心率互为倒数,且内切于圆x2+y2=4.
(a>b>0)的离心率与双曲线x2-y2=1的离心率互为倒数,且内切于圆x2+y2=4. x+m交椭圆于A、B两点,椭圆上一点
x+m交椭圆于A、B两点,椭圆上一点 ,求△PAB面积的最大值.
,求△PAB面积的最大值.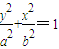 (a>b>0)的离心率与双曲线x2-y2=1的离心率互为倒数,且内切于圆x2+y2=4.
(a>b>0)的离心率与双曲线x2-y2=1的离心率互为倒数,且内切于圆x2+y2=4. x+m交椭圆于A、B两点,椭圆上一点
x+m交椭圆于A、B两点,椭圆上一点 ,求△PAB面积的最大值.
,求△PAB面积的最大值. (a>b>0)的离心率为
(a>b>0)的离心率为 ,长轴长为
,长轴长为 ,设过右焦点F倾斜角为θ的直线交椭圆M于A,B两点.
,设过右焦点F倾斜角为θ的直线交椭圆M于A,B两点.