题目内容
设f(x)= ,
, =(2cosx,1),
=(2cosx,1), =(cosx,
=(cosx, sin2x),x∈R.
sin2x),x∈R.
(I)若f(x)=0且x∈[- ,
, ],求x的值
],求x的值
(II)g(x)=cos(ωx- )+k与f(x)的最小正周期相同,g(x)经过(
)+k与f(x)的最小正周期相同,g(x)经过(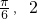 ),求g(x)的值域以及单调增区间.
),求g(x)的值域以及单调增区间.
解:(I)f(x)=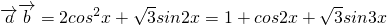
=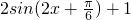
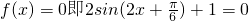
得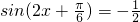
又因为x∈[- ,
, ],所以
],所以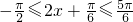
可得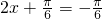 ,所以
,所以
(II)由(I)知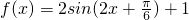
因为g(x)与f(x)的最小正周期相同
所以ω=2,又因为g(x)图象经过(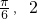 ),
),
∴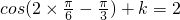
即1+k=2,故k=1
所以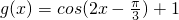 ,因此g(x)的值域为[0,2]
,因此g(x)的值域为[0,2]
再解不等式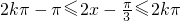 得,
得,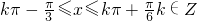
所以函数g(x)的单调增区间为[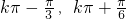 ],其中k∈Z
],其中k∈Z
分析:(I)由平面向量数量积的坐标表达式,得出f(x)的解析式,将其化为形如Asin(ωx+φ)+k(A、ω、φ、k是常数)的形式,再解方程f(x)=0可得x的值;
(II)由f(x)的周期,得出g(x)的ω值,再解方程g( )=2,解出k的值,可以得出g(x)的表达式,最后利用余弦函数的图象与性质可得g(x)的值域以及单调增区间.
)=2,解出k的值,可以得出g(x)的表达式,最后利用余弦函数的图象与性质可得g(x)的值域以及单调增区间.
点评:本题考查了三角函数的综合题,关键是利用三角恒等变换的公式对解析式进行化简,再由条件进行求角的三角函数值,考查了知识的综合应用能力.
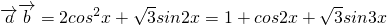
=
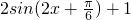
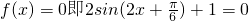
得
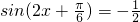
又因为x∈[-
 ,
, ],所以
],所以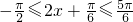
可得
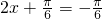 ,所以
,所以
(II)由(I)知
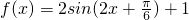
因为g(x)与f(x)的最小正周期相同
所以ω=2,又因为g(x)图象经过(
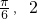 ),
),∴
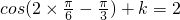
即1+k=2,故k=1
所以
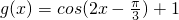 ,因此g(x)的值域为[0,2]
,因此g(x)的值域为[0,2]再解不等式
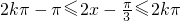 得,
得,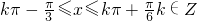
所以函数g(x)的单调增区间为[
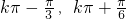 ],其中k∈Z
],其中k∈Z分析:(I)由平面向量数量积的坐标表达式,得出f(x)的解析式,将其化为形如Asin(ωx+φ)+k(A、ω、φ、k是常数)的形式,再解方程f(x)=0可得x的值;
(II)由f(x)的周期,得出g(x)的ω值,再解方程g(
 )=2,解出k的值,可以得出g(x)的表达式,最后利用余弦函数的图象与性质可得g(x)的值域以及单调增区间.
)=2,解出k的值,可以得出g(x)的表达式,最后利用余弦函数的图象与性质可得g(x)的值域以及单调增区间.点评:本题考查了三角函数的综合题,关键是利用三角恒等变换的公式对解析式进行化简,再由条件进行求角的三角函数值,考查了知识的综合应用能力.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目