题目内容
已知 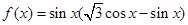
(Ⅰ)求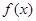 的单调增区间;(Ⅱ)当
的单调增区间;(Ⅱ)当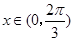 时,求
时,求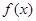 的取值范围.
的取值范围.
(Ⅰ)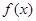 的单调增区间为
的单调增区间为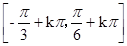 ;(Ⅱ)
;(Ⅱ)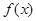 的取值范围是
的取值范围是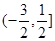 .
.
解析试题分析:(Ⅰ)将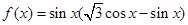 降次化一,化为
降次化一,化为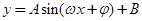 的形式,然后利用正弦函数的单调区间,即可求得其单调递增区间.
的形式,然后利用正弦函数的单调区间,即可求得其单调递增区间.
(Ⅱ)由(Ⅰ)可得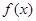
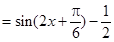 ,又
,又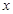 的范围为
的范围为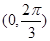 ,由此可得
,由此可得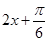 的范围,进而求得
的范围,进而求得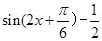 的范围.
的范围.
试题解析:(Ⅰ)因为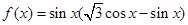
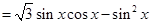
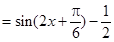 4分
4分
解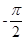 +2k
+2k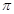
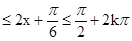 6分
6分
得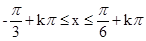 ,k
,k Z 7分
Z 7分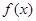 的单调增区间为
的单调增区间为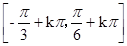 ,k
,k Z8分
Z8分
(Ⅱ)因为 , 9分
, 9分
所以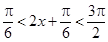 . 10分
. 10分
所以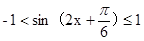 12分
12分
所以-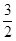 <sin(2x+
<sin(2x+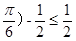
所以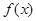 的取值范围是
的取值范围是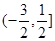 . 13分
. 13分
考点:1、三角恒等变换;2、三角函数的单调区间及范围..

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
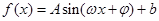 (
(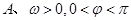 ,
,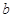 为常数)一段图像如图所示.
为常数)一段图像如图所示.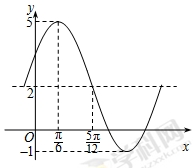
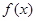 的解析式;
的解析式;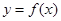 的图像向左平移
的图像向左平移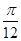 个单位,再将所得图像上各点的横坐标扩大为原来的4倍,得到函数
个单位,再将所得图像上各点的横坐标扩大为原来的4倍,得到函数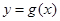 的图像,求函数
的图像,求函数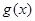 的单调递增区间.
的单调递增区间.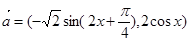 ,
,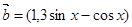 ,
,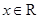 ,函数
,函数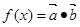 .
.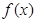 的最小正周期;
的最小正周期;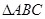 中,角
中,角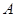 、
、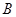 、
、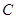 所对的边分别为
所对的边分别为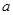 、
、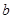 、
、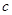 ,
,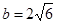 ,
, ,
,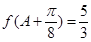 ,求
,求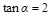 ,求下列各式的值:(1)
,求下列各式的值:(1) ;(2)
;(2)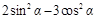 .
.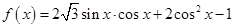 .
. 的单调递增区间;
的单调递增区间;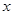 的方程
的方程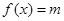 在区间
在区间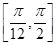 上有两个不同的实数根,求实数
上有两个不同的实数根,求实数 的取值范围.
的取值范围.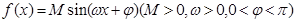 在一个周期上的系列对应值如下表:
在一个周期上的系列对应值如下表: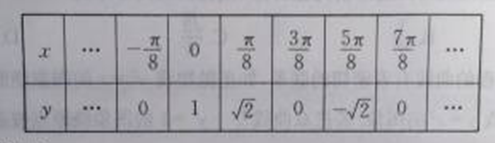
 的表达式;
的表达式; 的三个内角
的三个内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,且满足
,且满足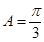 ,
,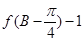 ,
,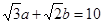 ,求边长
,求边长
 的值域,并写出函数
的值域,并写出函数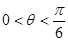 ,且
,且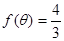 ,计算
,计算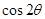 的值.
的值.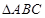 中,角A,B,C所对的边分别为
中,角A,B,C所对的边分别为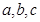 .
.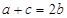 ,
,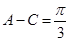 ,求
,求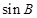 的值.
的值.
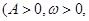
 的部分图象
的部分图象
 的解析式
的解析式  且
且 求
求 的值
的值