题目内容
(本小题满分12分)已知函数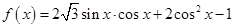 .
.
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)若关于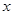 的方程
的方程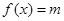 在区间
在区间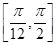 上有两个不同的实数根,求实数
上有两个不同的实数根,求实数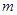 的取值范围.
的取值范围.
(Ⅰ) ,(Ⅱ)
,(Ⅱ)
解析试题分析:(Ⅰ)先将函数化简,化简时先用2倍角公式降幂,在将角统一,最后用化一公式化简成 的形式。再将
的形式。再将 代入正弦增区间公式即可。(Ⅱ)由(Ⅰ)知
代入正弦增区间公式即可。(Ⅱ)由(Ⅰ)知 ,所以
,所以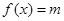 在区间
在区间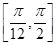 上有两个不同的实数根等价于
上有两个不同的实数根等价于 和
和 的图像有两个交点,利用数形结合即可解决此题。
的图像有两个交点,利用数形结合即可解决此题。
试题解析:(Ⅰ)




由 解得
解得 


所以 的递增区间是:
的递增区间是:
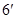
(Ⅱ)因为 ,所以
,所以
令
“关于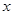 的方程
的方程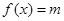 在
在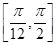 内有两个不同的实数根”等价于“函数
内有两个不同的实数根”等价于“函数 ,
, 和
和 的图象有两个不同的交点”.
的图象有两个不同的交点”. 
在同一直角坐标系中作出函数 ,
, 和
和 的图象如下:
的图象如下:

由图象可知:要使“函数 ,
, 和
和 的图象有两个不
的图象有两个不
同的交点”,必有 ,即
,即
因此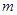 的取值范围是
的取值范围是 .
. 
考点:三角函数的单调性和图像

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
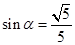 ,且
,且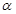 是第一象限角.
是第一象限角.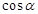 的值;
的值;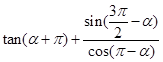 的值.
的值.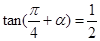 .
.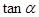 的值;
的值; 的值.
的值. ,
, .
. 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;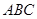 中,若
中,若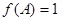 ,
,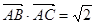 ,求△
,求△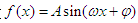 (其中
(其中 )的图象如图所示,把函数
)的图象如图所示,把函数 的图像向右平移
的图像向右平移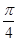 个单位,再向下平移1个单位,得到函数
个单位,再向下平移1个单位,得到函数 的图像.
的图像.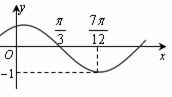
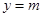 与函数
与函数 图像在
图像在 时有两个公共点,其横坐标分别为
时有两个公共点,其横坐标分别为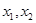 ,求
,求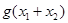 的值;
的值; 内角
内角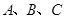 的对边分别为
的对边分别为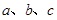 ,且
,且
 .若向量
.若向量 与
与 共线,求
共线,求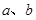 的值.
的值.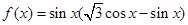
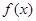 的单调增区间;(Ⅱ)当
的单调增区间;(Ⅱ)当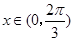 时,求
时,求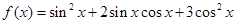 ,
,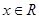 .求:
.求: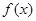 的最小值及取得最小值的自变量
的最小值及取得最小值的自变量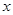 的集合;
的集合; 为坐标原点,
为坐标原点, ,
, .
.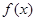 的定义域为
的定义域为 ,求
,求 的单调递增区间;
的单调递增区间; ,值域为
,值域为 ,求
,求 的值.
的值. .
. ,求
,求 的值;
的值; ,求
,求 的最大值.
的最大值.