题目内容
【题目】设椭圆
的方程为
，点
为坐标原点，点
，
的坐标分别为
，
，
，直线
的斜率为
.
（1）求椭圆的方程；
（2）若斜率为
的直线
交椭圆于
，
两点，交
轴于点
，问是否存在实数
使得以
为直径的圆恒过点？若存在，求的值；若不存在，说明理由.
【答案】（1）
（2）存在；
【解析】
（1）根据题意，设点
的坐标为
，可得
，进而可得椭圆
的方程；
（2）根据题意，设直线
的方程为
，联立方程，通过韦达定理，假设存在实数
，使得以
为直径的圆恒过点
，即可得
，利用向量数量积为
，解得即可.
（1）设点的坐标为，
，
，
，又
，
，
椭圆的方程为.
（2）依题意，设直线的方程为，代入，
得
.
设
，
，则
，
.
假设存在实数，使得以为直径的圆恒过点，则.
又
，
，
∴
，
即
，将，代入，整理得
，解得
，
即当时，存在实数使得以为直径的圆恒过点.
练习册系列答案
相关题目
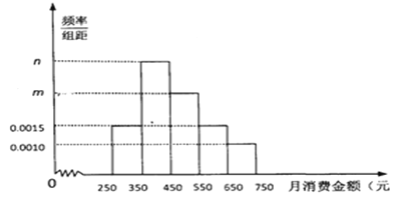
【题目】某同学为研究“网络游戏对当代青少年的影响”作了一次调查，共调查了50名同学，其中男生26人，有8人不喜欢玩游戏，而调查的女生中有9人喜欢玩游戏.
（1）根据以上数据完成2×2的列联表；
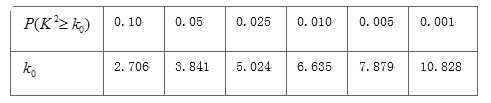
（2）根据以上数据，在犯错误的概率不超过0.025的前提下，能否认为“喜欢玩电脑游戏与性别有关系”？
男生 | 女生 | 总计 | |
喜欢玩游戏 | |||
不喜欢玩游戏 | |||
总计 |
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
