题目内容
已知f(x)=2+log3x,x∈[1,3].求: 函数y=[f(x)]2+f(x2)的值域.
解:y=[f(x)]2+f(x2)=(log3x)2+6log3x+6,
∵x∈[1,3],∴ ∴1≤x≤
∴1≤x≤![]() ,
,
∴y=log32x+6log3x+6 (1≤x≤![]() ).
).
令t=log3x,由x∈[1,![]() ]得t∈[0,
]得t∈[0,![]() ].
].
∴y=t2+6t+6,t∈[0,![]() ]=(t+3)2-3,
]=(t+3)2-3,
∵t∈[0,![]() ]为y的增区间,
]为y的增区间,
∴当t=0时,ymin=6.
当t=![]() 时,ymax=
时,ymax=![]() ,
,
∴函数值域为[6,![]() ].
].

练习册系列答案
相关题目
 (2012•潍坊二模)如图,已知F(2,0)为椭圆
(2012•潍坊二模)如图,已知F(2,0)为椭圆 R),
R), =
2x2+3x-1,h (x)为f
(x)、g(x)在R上生成的一个二次函数.
=
2x2+3x-1,h (x)为f
(x)、g(x)在R上生成的一个二次函数. ,若h (x)为偶函数,求
,若h (x)为偶函数,求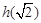 ;
; ,若h (x)同时也是g(x)、l(x) 在R上生成的一个函数,求a+b的最小值;
,若h (x)同时也是g(x)、l(x) 在R上生成的一个函数,求a+b的最小值;