题目内容
已知函数
(1)若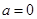 ,解不等式
,解不等式 ;
;
(2)解关于 的不等式
的不等式
【答案】
(1)
(2)当 时,原不等式的解集为
时,原不等式的解集为 ;
;
当 时,原不等式的解集为
时,原不等式的解集为 ;
;
当 时,原不等式的解集为
时,原不等式的解集为 ;
;
当 时,原不等式的解集为
时,原不等式的解集为 ;
;
当 时,原不等式的解集为
时,原不等式的解集为 ;
;
【解析】
试题分析:解:(1)

 ,
,
故解得原不等式的解集为 ;
.4分
;
.4分
(2)原式






 且
且 , 6分
, 6分
当 ,即
,即 时,原不等式
时,原不等式
 且
且 ,
,
解得 7分
7分
当 ,即
,即 时,原不等式
时,原不等式
 8分
8分
当 ,即
,即 时,原不等式
时,原不等式
 且
且 , 9分
, 9分
?当 时,
时, ,解出
,解出 ;
;
?当 时,
时,
 ;
10分
;
10分
?当 时,
时, ,解出
,解出 ; 11分
; 11分
综上:当 时,原不等式的解集为
时,原不等式的解集为 ;
;
当 时,原不等式的解集为
时,原不等式的解集为 ;
;
当 时,原不等式的解集为
时,原不等式的解集为 ;
;
当 时,原不等式的解集为
时,原不等式的解集为 ;
;
当 时,原不等式的解集为
时,原不等式的解集为 ;
12分
;
12分
考点:一元二次不等式的解集
点评:主要是考查了一元二次不等式的解集的求解,以及分类讨论思想的运用,属于中档题。

练习册系列答案
相关题目

 的表达式;
的表达式; 上是单调函数.
上是单调函数.
 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值; 的图象与函数
的图象与函数
 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值; 的图象与函数
的图象与函数
 ,求
,求 的零点;
的零点; 上有两个不同的零点,求
上有两个不同的零点,求 的取值范围。
的取值范围。