题目内容
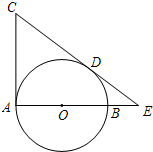 (2012•昌平区二模)如图,AB是⊙O的直径,CD切⊙O于点D,CA切⊙O于点A,CD交AB的延长线于点E.若AC=3,ED=2,则BE=
(2012•昌平区二模)如图,AB是⊙O的直径,CD切⊙O于点D,CA切⊙O于点A,CD交AB的延长线于点E.若AC=3,ED=2,则BE=1
1
;AO=| 3 |
| 2 |
| 3 |
| 2 |
分析:连接OD,设圆半径为r,由AB是⊙O的直径,CD切⊙O于点D,CA切⊙O于点A,CD交AB的延长线于点E.AC=3,ED=2,知OD2+DE2=OE2,△ACE∽△DOE,由此能求出结果.
解答: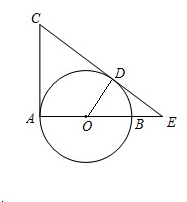 解:连接OD,设圆半径为r,
解:连接OD,设圆半径为r,
∵AB是⊙O的直径,CD切⊙O于点D,CA切⊙O于点A,CD交AB的延长线于点E.AC=3,ED=2,
∴OD2+DE2=OE2,△ACE∽△DOE,
∴r2+4=(BE+r)2,①
=
,②
联立①②,解得BE=1,AO=r=
.
故答案为:1,
.
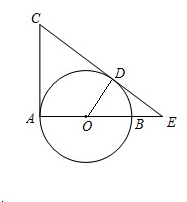 解:连接OD,设圆半径为r,
解:连接OD,设圆半径为r,∵AB是⊙O的直径,CD切⊙O于点D,CA切⊙O于点A,CD交AB的延长线于点E.AC=3,ED=2,
∴OD2+DE2=OE2,△ACE∽△DOE,
∴r2+4=(BE+r)2,①
| 2r+BE |
| 2 |
| 3 |
| r |
联立①②,解得BE=1,AO=r=
| 3 |
| 2 |
故答案为:1,
| 3 |
| 2 |
点评:本题考查与圆有关的比例线段的求法,是基础题.解题时要认真审题,仔细解答,注意三角形相似和勾股定理的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•昌平区二模)已知空间几何体的三视图如图所示,则该几何体的各侧面图形中,是直角三角形的有( )
(2012•昌平区二模)已知空间几何体的三视图如图所示,则该几何体的各侧面图形中,是直角三角形的有( ) (2012•昌平区二模)在正四棱柱ABCD-A1B1C1D1中,AA1=2AB=2,E为AD中点,F为CC1中点.
(2012•昌平区二模)在正四棱柱ABCD-A1B1C1D1中,AA1=2AB=2,E为AD中点,F为CC1中点.