题目内容
（2012•昌平区二模）已知空间几何体的三视图如图所示，则该几何体的各侧面图形中，是直角三角形的有（ ）分析：本题由三视图可知原几何体是一个四棱锥，由线面垂直的判定，可证AB⊥AP，故△PAB为直角三角形，同理，△PCD也为直角三角形，故可得答案．
解答：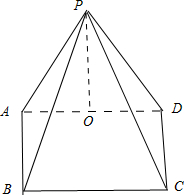
解：由三视图可知原几何体是一个四棱锥，
并且顶点P在下底面的射影点为正方形边AD的中点O，
所以PO⊥底面ABCD，可得PO⊥AB，又AB⊥AD，AB∩PO=O，
由线面垂直的判定可得AB⊥平面PAD，可证AB⊥AP，故△PAB为直角三角形，
∵CD∥AB，∴CD⊥平面PAD，CD⊥PD，即△PCD也为直角三角形．
故左右侧面均为直角三角形，而前后侧面PBC与PAD均为非直角的等腰三角形．
所以侧面中直角三角形个数为2个，
故选C
解：由三视图可知原几何体是一个四棱锥，并且顶点P在下底面的射影点为正方形边AD的中点O，
所以PO⊥底面ABCD，可得PO⊥AB，又AB⊥AD，AB∩PO=O，
由线面垂直的判定可得AB⊥平面PAD，可证AB⊥AP，故△PAB为直角三角形，
∵CD∥AB，∴CD⊥平面PAD，CD⊥PD，即△PCD也为直角三角形．
故左右侧面均为直角三角形，而前后侧面PBC与PAD均为非直角的等腰三角形．
所以侧面中直角三角形个数为2个，
故选C
点评：本题为三视图的还原问题，只要作出原几何体，理清其中的线面关系即得的答案，属于基础题．
练习册系列答案
相关题目
（2012•昌平区二模）在正四棱柱ABCD-A1B1C1D1中，AA1=2AB=2，E为AD中点，F为CC1中点．