题目内容
已知命题p：“∀x∈[1,2]，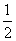
x2－lnx－a≥0”与命题q：“∃x0∈R，x
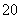＋2ax0－8－6a＝0”都是真命题，则实数a的取值范围是________．
(－∞，－4]∪[－2，]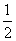
[解析] 若p真，则∀x∈[1,2]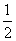，(x2－lnx)min≥a，
∵y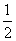＝x2－lnx的导数y′＝x－
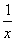≥0在[1,2]上恒成立，∴当x＝1时，ymin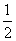＝，∴a≤；
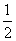若q真，则(2a)2－4×(－8－6a)＝4(a＋2)(a＋4)≥0，
∴a≤－4或a≥－2.
∴实数a的取值范围为(－∞，－4]∪[－2，]．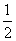
练习册系列答案
世纪百通期末金卷系列答案
相关题目
设
，则f（n+1）﹣f（n）=（ ）
|
| A． |
| B． |
|
|
| C． |
| D． |
|
＝1为双曲线；命题q：x2－7x＋12<0的解集是{x|3<x<4}．给出下列结论：①命题“p且q”是真命题；②命题“p且(綈q)”是假命题；③命题“(綈p)或q”是真命题；④命题“(綈p)或(綈q)”是假命题．其中正确的是( )
<x<
，则m的取值范围是________．
的定义域是( )