题目内容
等差数列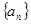 前
前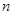 项和为
项和为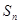 ,
,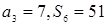 ,则公差d的值为
,则公差d的值为
| A.2 | B.3 | C.-3 | D.4 |
B
解析试题分析:根据题意,由于等差数列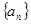 前
前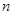 项和为
项和为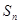 ,那么可设公差为d,则
,那么可设公差为d,则 ,故答案选B.
,故答案选B.
考点:等差数列的通项公式和求和
点评:解决的关键是根据数列的首项和公差联立方程组来得到基本量,进而求解,属于基础题。

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
在等差数列 中,若
中,若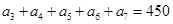 ,则
,则 的值等于( )
的值等于( )
| A.45 | B.75 | C.180 | D.300 |
在等差数列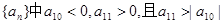 ,数列
,数列 的前
的前 项和为
项和为 ,则在
,则在 中最小的负数为 ( )
中最小的负数为 ( )
A.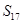 | B.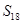 | C.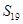 | D.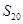 |
数列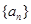 满足
满足 ,且
,且 ,则
,则
 ( ).
( ).
| A.29 | B.28 | C.27 | D.26 |
等差数列{an}共有2n+1项,其中奇数项之和为4,偶数项之和为3,则n的值是
| A.3 | B.5 | C.7 | D.9 |
等差数列{an} 中,a3 =2,则该数列的前5项的和为
| A.10 | B.16 | C.20 | D.32 |
在等差数列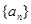 中,
中,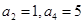 ,则
,则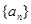 的前5项和
的前5项和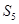 =( )
=( )
| A.7 | B.15 | C.20 | D.25 |
等差数列 中,若
中,若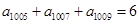 ,则该数列前2013项的和为
,则该数列前2013项的和为
A.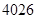 | B.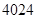 | C.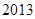 | D.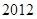 |
 满足:
满足: ,公差
,公差 . 若当且仅当
. 若当且仅当 时,数列
时,数列 项和
项和 取得最大值,则首项
取得最大值,则首项 的取值范围是( )
的取值范围是( )


