题目内容
在三棱锥S-ABC中,侧棱SA、SB、SC两两垂直且长度均为a,点H在BC上,且SH⊥BC,则sin∠HAS的值为
.
| ||
| 3 |
| ||
| 3 |
分析:取BC的中点,即为H,连接SH,AH,由题设条件推导出SA⊥SH,由此能在直角三角形SAH中,求出sin∠HAS的大小.
解答: 解:取BC的中点,即为H,连接SH,AH,
解:取BC的中点,即为H,连接SH,AH,
∵在三棱锥S-ABC中,SA=SC=SB=a,
SA⊥SB,SB⊥SC,SC⊥SA,
∴SA⊥平面SBC,
∵SH?平面SBC,
∴SA⊥SH,
在直角三角形SAH中,sin∠HAS=
=
=
故答案为:
.
 解:取BC的中点,即为H,连接SH,AH,
解:取BC的中点,即为H,连接SH,AH,∵在三棱锥S-ABC中,SA=SC=SB=a,
SA⊥SB,SB⊥SC,SC⊥SA,
∴SA⊥平面SBC,
∵SH?平面SBC,
∴SA⊥SH,
在直角三角形SAH中,sin∠HAS=
| SH |
| AH |
| ||||||
|
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题考查异面直线所成角的大小的求法,解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为1的等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为1的等边三角形,∠BAC=90°,O为BC中点.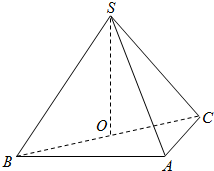 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点. 如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,
如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2, C.
C. 如图,在三棱锥S-ABC中,
如图,在三棱锥S-ABC中,