题目内容
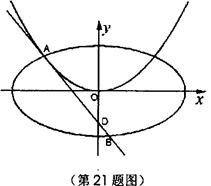
如图,已知过点D(0,-2)作抛物线C1: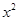 =2py(p>0)的切线l,切点A在第二象限.
=2py(p>0)的切线l,切点A在第二象限.
(Ⅰ)求点A的纵坐标;
(Ⅱ)若离心率为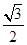 的椭圆
的椭圆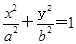 (a>b>0)恰好经过点A,设直线l交椭圆的另一点为B,记直线l,OA,OB的斜率分别为k,k1,k2,若k1+2k2=4k,求椭圆方程.
(a>b>0)恰好经过点A,设直线l交椭圆的另一点为B,记直线l,OA,OB的斜率分别为k,k1,k2,若k1+2k2=4k,求椭圆方程.
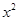 =2py(p>0)的切线l,切点A在第二象限.
=2py(p>0)的切线l,切点A在第二象限.(Ⅰ)求点A的纵坐标;
(Ⅱ)若离心率为
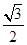 的椭圆
的椭圆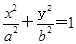 (a>b>0)恰好经过点A,设直线l交椭圆的另一点为B,记直线l,OA,OB的斜率分别为k,k1,k2,若k1+2k2=4k,求椭圆方程.
(a>b>0)恰好经过点A,设直线l交椭圆的另一点为B,记直线l,OA,OB的斜率分别为k,k1,k2,若k1+2k2=4k,求椭圆方程.
解:(Ⅰ)由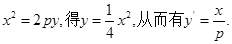 设切点
设切点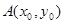 ,且
,且 ,由切线
,由切线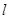 的斜率为
的斜率为 ,得
,得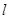 的方程为
的方程为 ,又点
,又点 在
在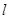 上,
上,
 ,即点
,即点 的纵坐标
的纵坐标
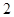 ..........4分
..........4分
(Ⅱ)由(Ⅰ)得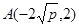 ,切线斜率
,切线斜率 ,
,
设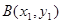 ,切线方程为
,切线方程为 ,由
,由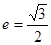 ,得
,得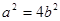 ,
,
所以椭圆方程为 ,且过
,且过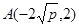 ,
, ……6分
……6分
由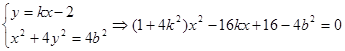 ,
,
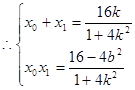 , ........8分
, ........8分

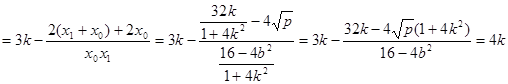
……….10分
将 ,
, 代入得:
代入得: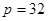 ,所以
,所以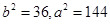 ,
,
椭圆方程为 . ……….12分
. ……….12分
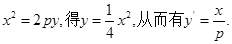 设切点
设切点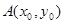 ,且
,且 ,由切线
,由切线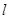 的斜率为
的斜率为 ,得
,得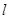 的方程为
的方程为 ,又点
,又点 在
在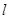 上,
上, ,即点
,即点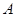 的纵坐标
的纵坐标
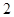 ..........4分
..........4分(Ⅱ)由(Ⅰ)得
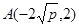 ,切线斜率
,切线斜率 ,
,设
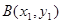 ,切线方程为
,切线方程为 ,由
,由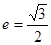 ,得
,得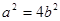 ,
,所以椭圆方程为
 ,且过
,且过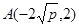 ,
, ……6分
……6分由
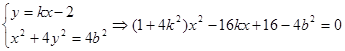 ,
,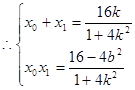 , ........8分
, ........8分
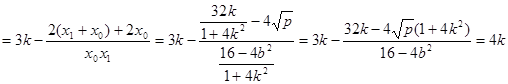
……….10分
将
 ,
, 代入得:
代入得: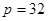 ,所以
,所以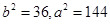 ,
,椭圆方程为
 . ……….12分
. ……….12分略

练习册系列答案
相关题目
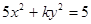 的一个焦点是(0,2),那么
的一个焦点是(0,2),那么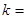 ( )
( )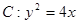 ,顶点为O,动直线
,顶点为O,动直线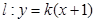 与抛物
与抛物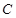 交于
交于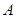 、
、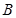 两点
两点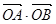 是一个与
是一个与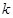 无关的常数;
无关的常数;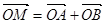 的点
的点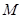 的轨迹方程。
的轨迹方程。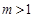 ,直线l:
,直线l: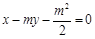 ,椭圆C:
,椭圆C: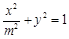 ,
,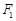 ,
,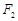 分别为椭圆C的左、右焦点。
分别为椭圆C的左、右焦点。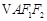 ,
,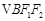 的重心分别为G,H。若原点O在以线段GH为直径的圆内,求实数
的重心分别为G,H。若原点O在以线段GH为直径的圆内,求实数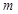 的取值范围。
的取值范围。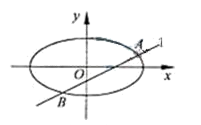
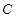 的方程为
的方程为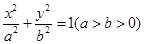 ,称圆心在坐标原点
,称圆心在坐标原点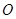 ,半径为
,半径为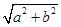 的圆为椭圆
的圆为椭圆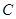 的“伴随圆”,椭圆
的“伴随圆”,椭圆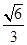 .
.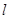 与椭圆
与椭圆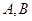 两点,与其“伴随圆”交于
两点,与其“伴随圆”交于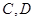 两点,当
两点,当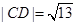 时,求△
时,求△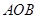 面积的最大值.
面积的最大值.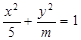 的离心率
的离心率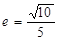 ,则
,则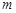 的值为:
的值为: 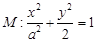
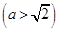 的右焦点为
的右焦点为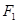 ,直线
,直线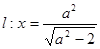 与
与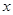 轴交于点
轴交于点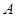 ,若
,若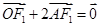 (其中
(其中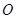 为坐标原点).
为坐标原点).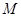
 的方程;
的方程;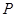 是椭圆
是椭圆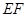 为圆
为圆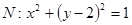 的任意一条直径(
的任意一条直径(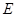 ,
,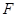 为直径的两个端点),求
为直径的两个端点),求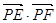 的最大值.
的最大值.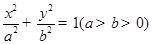 的左、右焦点分别为
的左、右焦点分别为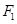 、
、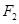 ,
,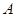 是椭圆上的一点,
是椭圆上的一点,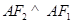 ,原点
,原点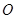 到直线
到直线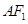 的距离为
的距离为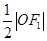 ,则椭圆的离心率为( )
,则椭圆的离心率为( )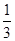
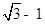
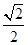
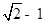
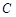 中心在原点,焦点在坐标轴上,直线
中心在原点,焦点在坐标轴上,直线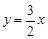 与椭圆
与椭圆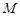 ,点
,点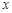 轴上的射影恰好是椭圆
轴上的射影恰好是椭圆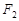 ,椭圆
,椭圆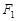 ,且
,且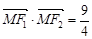
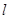 过点
过点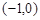 ,且与椭圆
,且与椭圆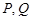 两点,求
两点,求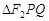 的内切圆面积的最大值
的内切圆面积的最大值