Question

设函数f(x)=

21-x，x≤0 f(x-1)，x＞0

，方程f（x）=x+a有且只有两不相等实数根，则实数a的取值范围为______．

Answer 1

∵x＞0时，f（x）=f（x-1）
∴当x＞0时，f（x）是周期函数，周期为1
设x＜1，则x-1＜0，
f（x）=f（x-1）=21^-（x-1）=2^2-x
即x＜1，f（x）=2^2-x
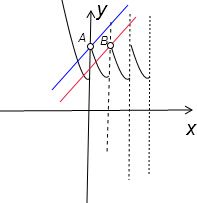
做出函数图象如下图
方程f（x）=x+a有且只有两不相等实数根，只要直线y=x+a介于图中两直线之间即可．
依f（x）=2^2-x可求出A点坐标为（0，4），B点坐标为（1，4）
∵A，B两点均为虚点
∴3≤a＜4
故答案为[3，4）．