题目内容
15.已知多项式x3+x10=a0+a1(x+1)+a2(x+1)2+…+a9(x+1)9+a10(x+1)10,则a2=( )| A. | 32 | B. | 42 | C. | 46 | D. | 56 |
分析 由条件利用x3+x10=[-1+(x+1)]3+[-1+(x+1)]10,即可求得a2的值.
解答 解:∵多项式x3+x10=[-1+(x+1)]3+[-1+(x+1)]10=a0+a1(x+1)+…+a9(x+1)9+a10(x+1)10,
∴a2=-${C}_{3}^{2}+{C}_{10}^{2}$=42,
故选:B
点评 本题主要考查二项式定理的应用,式子的变形是解题的关键,属于基础题.

练习册系列答案
相关题目
10.△ABC中,角A,B,C所对的边长分别为a,b,c,$\overrightarrow{m}$=$({a,\sqrt{3}b})$,$\overrightarrow{n}$=(sinB,cosA),$\overrightarrow{m}$⊥$\overrightarrow{n}$,b=2,$a=\sqrt{7}$,则△ABC的面积为( )
| A. | $\sqrt{3}$ | B. | $\frac{{3\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $2\sqrt{3}$ |
20.已知集合A={-1,1,2,},B={x|(x-1)(x-3)≤0},则A∩B=( )
| A. | .{1,2} | B. | {1} | C. | {-1,1} | D. | .∅ |
4.设点M(0,-5),N(0,5),△MNP的周长为36,则△MNP的顶点P的轨迹方程为( )
| A. | $\frac{{y}^{2}}{169}$+$\frac{{x}^{2}}{25}$=1(x≠0) | B. | $\frac{{y}^{2}}{169}$+$\frac{{x}^{2}}{144}$=1(x≠0) | ||
| C. | $\frac{{x}^{2}}{169}$+$\frac{{y}^{2}}{25}$=1(y≠0) | D. | $\frac{{y}^{2}}{169}$+$\frac{{x}^{2}}{25}$=1(y≠0) |
 如图,在边长为a的正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,现沿SE,SF及EF把这个正方形折成一个三棱锥,使G1,G2,G3三点重合,重合点记为G,则点G到平面SEF的距离为$\frac{a}{3}$.
如图,在边长为a的正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,现沿SE,SF及EF把这个正方形折成一个三棱锥,使G1,G2,G3三点重合,重合点记为G,则点G到平面SEF的距离为$\frac{a}{3}$.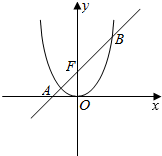 如图,已知抛物线C:x2=2py(0<p<4),其上一点M(4,y0)到其焦点F的距离为5,过焦点F的直线l与抛物线C交于A,B左、右两点.
如图,已知抛物线C:x2=2py(0<p<4),其上一点M(4,y0)到其焦点F的距离为5,过焦点F的直线l与抛物线C交于A,B左、右两点.