题目内容
(1)求证:直线(2+m)x+(1-2m)y+4-3m=0,不论m为何实数,此直线必过定点;(2)过这定点引一直线,使它夹在两坐标轴间的线段被这点平分,求这条直线的方程.
(1)证明:(2+m)x+(1-2m)y+4-3m=0,
∴(x-2y-3)m+2x+y+4=0.
上式为关于m的恒等式,当满足:![]() 时,m为任何实数均成立.
时,m为任何实数均成立.
解得![]()
∴直线必过定点(-1,-2).
(2)解:设直线交两坐标轴于A(a,0)、B(0,b),则由AB线段被(-1,-2)平分,
∴
∴![]()
∴直线过(-2,0),(0,-4).故直线方程为2x+y+4=0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
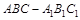 中,
中, 平面
平面 ,其垂足
,其垂足 落在直线
落在直线 上.
上.
 ;
;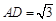 ,
, ,
,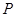 为
为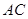 的中点,求三棱锥
的中点,求三棱锥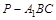 的体积.
的体积.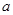 的正方形,且PD=
的正方形,且PD=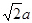 .
.