题目内容
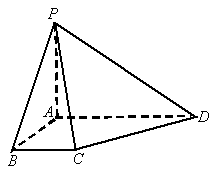
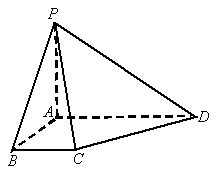
如图,在四棱椎P-ABCD中,底面ABCD是边长为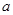 的正方形,且PD=
的正方形,且PD=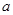 ,PA=PC=
,PA=PC=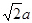 .
.
(1)求证:直线PD⊥面ABCD;
(2)求二面角A-PB-D的大小.

【答案】
(1)见解析 (2)二面角A-PB-D的平面角为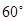
【解析】(1) 本小题可通过证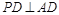 ,和
,和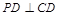 来达到证明直线PD⊥面ABCD的目的.(2)解决本小题的关键是作出二面角的平面角,取AP中点H,过H作
来达到证明直线PD⊥面ABCD的目的.(2)解决本小题的关键是作出二面角的平面角,取AP中点H,过H作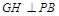 于G,连结DG.则
于G,连结DG.则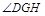 为所求二面角平面角,然后解三角形求角即可
为所求二面角平面角,然后解三角形求角即可
(1)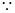 在
在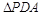 中,
中,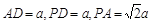 ,
,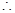
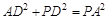 即
即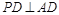 ,同理
,同理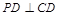 又AD、CD
又AD、CD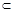 平面ABCD,
平面ABCD,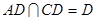
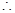 直线PD
直线PD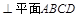 …5分
…5分
(2)解法一:如图,连结AC和BD,设
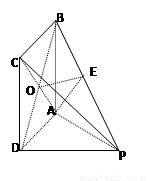
由(1)知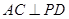 ,又
,又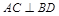 ,且PD、BD
,且PD、BD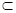 平面PBD,
平面PBD,
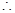 直线AC
直线AC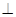 平面PBD,………6分
平面PBD,………6分
过点O作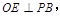 E为垂足,连结AE,由三垂线定理知
E为垂足,连结AE,由三垂线定理知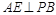 ,
,
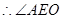 为二面角A-PB-D的平面角………8分
为二面角A-PB-D的平面角………8分
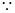 AB
AB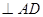 ,所以
,所以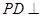 面ABCD,故AB
面ABCD,故AB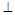 PD,从而AB
PD,从而AB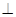 面PAD,故AB
面PAD,故AB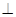 PA,
PA,
 在
在 中,
中,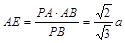 ………………10分
………………10分
 在
在 中,
中,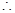
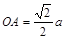
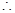 在
在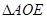 中,
中,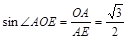
 二面角A-PB-D的平面角为
二面角A-PB-D的平面角为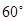 .…………12分
.…………12分
解法二:取AP中点H,过H作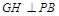 于G,连结DG
于G,连结DG

则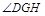 为所求二面角平面角,
为所求二面角平面角, 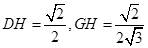
解法三:利用空间向量

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在四棱椎P-ABCD中,底面ABCD是∠BAD=60°且边长为2的菱形,侧面PAD为正三角形,其所在平面垂直于底面ABCD.
如图,在四棱椎P-ABCD中,底面ABCD是∠BAD=60°且边长为2的菱形,侧面PAD为正三角形,其所在平面垂直于底面ABCD. 如图,在四棱椎P-ABCD中,底面ABCD是∠BAD=60°且边长为2的菱形,侧面PAD为正三角形,其所在平面垂直于底面ABCD.
如图,在四棱椎P-ABCD中,底面ABCD是∠BAD=60°且边长为2的菱形,侧面PAD为正三角形,其所在平面垂直于底面ABCD.