题目内容
函数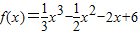
在区间[-1，3]内的最小值是 ．
【答案】分析：根据函数的解析式选择求导判断函数的单调性，再求函数的最值．
解答：解：
，所以f′（x）=x2-x-2=（x-2）（x+1），
所以当-1≤x≤2时，f′（x）＜0，当2＜x≤3时，f′（x）＞0，
因此函数在[-1，2]上单调递减，在[2，3]上单调递增，
所以函数在x=2时取得最小值，最小值为
，
故答案为
．
点评：本题考察函数最值的求解，由于函数的最高次幂为3，故需要先利用导数判断函数的单调性，再求最值．
解答：解：
，所以f′（x）=x2-x-2=（x-2）（x+1），所以当-1≤x≤2时，f′（x）＜0，当2＜x≤3时，f′（x）＞0，
因此函数在[-1，2]上单调递减，在[2，3]上单调递增，
所以函数在x=2时取得最小值，最小值为
，故答案为
．点评：本题考察函数最值的求解，由于函数的最高次幂为3，故需要先利用导数判断函数的单调性，再求最值．
练习册系列答案
相关题目
已知函数f（x）=x2+2，则该函数在区间[1，3]上的平均变化率为（ ）
| A、4 | B、3 | C、2 | D、1 |
，
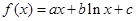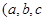是常数）在x=e处的切线方程为
，
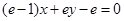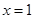既是函数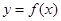
的零点，又是它的极值点．
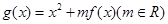在区间(1，3)内不是单调函数，求实数m的取值范围；
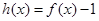的单调递减区间，并证明：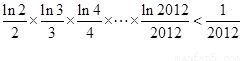
≤
≤1，若函数
在区间[1，3]上的最大值为
，最小值为
，令
．
的函数表达式；