题目内容
15. 在等腰直角△ABC中,∠A=90°,BC=6,△ABC中排列着内接正方形,如图所示,若正方形的面积依次为S1,S2,…,Sn,…(从大到小),其中n∈N+,则$\underset{lim}{n→∞}$(S1+S2+…+Sn)=$\frac{9}{2}$.
在等腰直角△ABC中,∠A=90°,BC=6,△ABC中排列着内接正方形,如图所示,若正方形的面积依次为S1,S2,…,Sn,…(从大到小),其中n∈N+,则$\underset{lim}{n→∞}$(S1+S2+…+Sn)=$\frac{9}{2}$.
分析 通过相似三角形的相似比可知任意两个正方形的边长比为定值,进而计算可知Sn=$\frac{4}{{9}^{n-1}}$,求和取极限即可.
解答 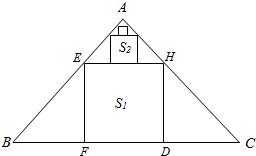 解:设最大的内接正方形EFDH的边长为x,
解:设最大的内接正方形EFDH的边长为x,
∵△ABC是等腰直角三角形,∠A=90°,
∴∠B=∠C=45°,
∴∠BEF=∠CHD=∠FBE=∠DCH=45°,
∴AE=$\frac{\sqrt{2}}{2}$x,BE=$\sqrt{2}$x,
∴AB=$\frac{3\sqrt{2}}{2}$x,
∴$\frac{EH}{BC}$=$\frac{AE}{AB}$=$\frac{1}{3}$,
又∵BC=6,
∴$\sqrt{{S}_{1}}$=EH=2,
∴数列{$\sqrt{{S}_{n}}$}构成首项为2,公比为$\frac{1}{3}$的等比数列,
∴Sn=$(\frac{2}{{3}^{n-1}})^{2}$=$\frac{4}{{9}^{n-1}}$,
∴$\underset{lim}{n→∞}$(S1+S2+…+Sn)=$\underset{lim}{n→∞}$$\frac{4(1-\frac{1}{{9}^{n}})}{1-\frac{1}{9}}$=$\underset{lim}{n→∞}$($\frac{9}{2}$-$\frac{1}{2}$•$\frac{1}{{9}^{n-1}}$)=$\frac{9}{2}$,
故答案为:$\frac{9}{2}$.
点评 本题考查数列的通项及前n项和,考查极限思想,找出数列的公比是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
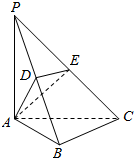 在三棱锥P-ABC中,PA⊥面ABC,∠ABC=90°,若AD⊥PB,垂足为D,AE⊥PC,垂足为E,求证:AD⊥PC.
在三棱锥P-ABC中,PA⊥面ABC,∠ABC=90°,若AD⊥PB,垂足为D,AE⊥PC,垂足为E,求证:AD⊥PC.