题目内容
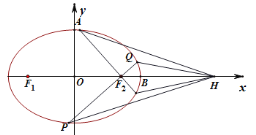
【题目】如图，在平面直角坐标系中，已知椭圆C：
(a＞b＞0)的短轴长为2，F1，F2分别是椭圆C的左、右焦点，过点F2的动直线与椭圆交于点P，Q，过点F2与PQ垂直的直线与椭圆C交于A、B两点.当直线AB过原点时，PF1＝3PF2.
（1）求椭圆的标准方程；
（2）若点H(3，0)，记直线PH，QH，AH，BH的斜率依次为
，
，
，
.
①若
，求直线PQ的斜率；
②求
的最小值.
【答案】（1）
（2）①
或
②
【解析】
（1）已知条件有
，直线AB过原点时，PQx轴，所以△PF1F2为直角三角形，利用椭圆定义和勾股定理可求得
，得椭圆方程；
（2）①设直线PQ：
，代入到椭圆方程得后化简，设P(
，
)，Q(
，
)，应用韦达定理得
，
，计算
并代入
可得；
②分类讨论，当这两条直线中有一条与坐标轴垂直时，
，
当两条直线与坐标轴都不垂直时，由①知
，同理可得
，计算
后应用基本不等式可得最小值．
解：（1）因为椭圆C：
(a＞b＞0)的短轴长为2，所以b＝1，
当直线AB过原点时，PQx轴，所以△PF1F2为直角三角形，
由定义知PF1＋PF2＝2a，而PF1＝3PF2，故
，
，
由
得
，化简得a2＝2，
故椭圆的方程为.
（2）①设直线PQ：，代入到椭圆方程得：
，设P(，)，Q(，)，则，，
所以
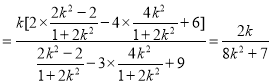
所以
，
解得：
或
，即为直线PQ的斜率.
②当这两条直线中有一条与坐标轴垂直时，，
当两条直线与坐标轴都不垂直时，
由①知，同理可得
故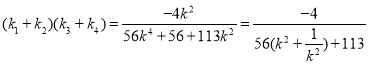
，
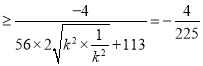当且仅当
即k＝1时取等号.
综上，的最小值为.
练习册系列答案
计算高手系列答案
相关题目
