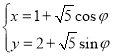题目内容
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,离心率为
,离心率为![]() ,
,![]() 是椭圆上的一个动点(不与左、右顶点重合),且
是椭圆上的一个动点(不与左、右顶点重合),且![]() 的周长为6,点
的周长为6,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,直线
,直线![]() 交于点
交于点![]() .
.
(1)求椭圆方程;
(2)若直线![]() 与椭圆交于另一点
与椭圆交于另一点![]() ,且
,且![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)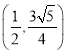 或
或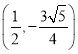
【解析】
(1)根据![]() 的周长为
的周长为![]() ,结合离心率,求出
,结合离心率,求出![]() ,即可求出方程;
,即可求出方程;
(2)设![]() ,则
,则![]() ,求出直线
,求出直线![]() 方程,若
方程,若![]() 斜率不存在,求出
斜率不存在,求出![]() 坐标,直接验证是否满足题意,若
坐标,直接验证是否满足题意,若![]() 斜率存在,求出其方程,与直线
斜率存在,求出其方程,与直线![]() 方程联立,求出点
方程联立,求出点![]() 坐标,根据
坐标,根据![]() 和
和![]() 三点共线,将点
三点共线,将点![]() 坐标用
坐标用![]() 表示,
表示,![]() 坐标代入椭圆方程,即可求解.
坐标代入椭圆方程,即可求解.
(1)因为椭圆的离心率为![]() ,
,![]() 的周长为6,
的周长为6,
设椭圆的焦距为![]() ,则
,则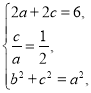
解得![]() ,
,![]() ,
,![]() ,
,
所以椭圆方程为![]() .
.
(2)设![]() ,则
,则![]() ,且
,且![]() ,
,
所以![]() 的方程为
的方程为![]() ①.
①.
若![]() ,则
,则![]() 的方程为
的方程为![]() ②,由对称性不妨令点
②,由对称性不妨令点![]() 在
在![]() 轴上方,
轴上方,
则![]() ,
,![]() ,联立①,②解得
,联立①,②解得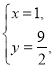 即
即![]() .
.
![]() 的方程为
的方程为![]() ,代入椭圆方程得
,代入椭圆方程得
![]() ,整理得
,整理得![]() ,
,
![]() 或
或![]() ,
,![]() .
.
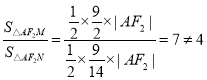 ,不符合条件.
,不符合条件.
若![]() ,则
,则![]() 的方程为
的方程为![]() ,
,
即![]() ③.
③.
联立①,③可解得![]() 所以
所以![]() .
.
因为![]() ,设
,设![]()
所以![]() ,即
,即![]() .
.
又因为![]() 位于
位于![]() 轴异侧,所以
轴异侧,所以![]() .
.
因为![]() 三点共线,即
三点共线,即![]() 应与
应与![]() 共线,
共线,
![]()
所以![]() ,即
,即![]() ,
,
所以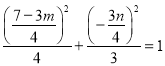 ,又
,又![]() ,
,
所以![]() ,解得
,解得![]() ,所以
,所以![]() ,
,
所以点![]() 的坐标为
的坐标为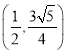 或
或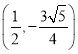 .
.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目