题目内容
已知函数 .
.(1)化简f(x);
(2)已知常数ω>0,若函数y=f(ωx)在区间
 上是增函数,求ω的取值范围;
上是增函数,求ω的取值范围;(3)若方程f(x)(sinx-1)+a=0有解,求实数a的取值范围.
【答案】分析:(1)利用二倍角的余弦公式和平方差公式整理函数式,再合并同类型,点的三角函数的最简形式.
(2)根据上一问做出的函数的解析式,代入自变量整理出函数式,根据正弦函数的单调性先写出函数的单调区间,根据所给的单调区间,两者进行比较,得到ω的取值范围.
(3)原方程可化为2sin2x-sinx+a-1=0,换元令sinx=t,则问题转化为方程2t2-t+a-1=0在[-1,1]内有一解或两解,根据解的情况写出实根分布的充要条件,得到结果.
解答:解:(1) =(2+2sinx)sinx+1-2sin2x=2sinx+1(14分)
=(2+2sinx)sinx+1-2sin2x=2sinx+1(14分)
(2)∵f(ωx)=2sinωx+1
由
∴f(ωx)的递增区间为
∵f(ωx)在 上是增函数
上是增函数
∴当k=0时,有
∴ 解得
解得 
∴ω的取值范围是 (8分)
(8分)
(3)解一:方程f(x)(sinx-1)+a=0即为(2sinx+1)(sinx-1)+a=0从而问题转化为方程a=-2sin2x+sinx+1有解,只需a在函数y=-2sin2x+sinx+1的值域范围内
∵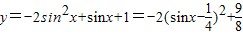
当 ;
;
当sinx=-1时,ymin=-2
∴实数a的取值范围为 (12分)
(12分)
解二:原方程可化为2sin2x-sinx+a-1=0
令sinx=t,则问题转化为方程2t2-t+a-1=0在[-1,1]内有一解或两解,
设g(t)=2t2-t+a-1,若方程在[-1,1]内有一个解,则 解得-2≤a<0
解得-2≤a<0
若方程在[-1,1]内有两个解,则 解得
解得
∴实数a的取值范围是[-2, ]
]
点评:本题考查三角函数的化简求值及一元二次方程的实根分布,本题解题的关键是整理出三角函数的解析式,熟练应用三角函数的公式来解题,本题是一个中档题目.
(2)根据上一问做出的函数的解析式,代入自变量整理出函数式,根据正弦函数的单调性先写出函数的单调区间,根据所给的单调区间,两者进行比较,得到ω的取值范围.
(3)原方程可化为2sin2x-sinx+a-1=0,换元令sinx=t,则问题转化为方程2t2-t+a-1=0在[-1,1]内有一解或两解,根据解的情况写出实根分布的充要条件,得到结果.
解答:解:(1)
 =(2+2sinx)sinx+1-2sin2x=2sinx+1(14分)
=(2+2sinx)sinx+1-2sin2x=2sinx+1(14分)(2)∵f(ωx)=2sinωx+1
由

∴f(ωx)的递增区间为

∵f(ωx)在
 上是增函数
上是增函数∴当k=0时,有

∴
 解得
解得 
∴ω的取值范围是
 (8分)
(8分)(3)解一:方程f(x)(sinx-1)+a=0即为(2sinx+1)(sinx-1)+a=0从而问题转化为方程a=-2sin2x+sinx+1有解,只需a在函数y=-2sin2x+sinx+1的值域范围内
∵
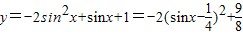
当
 ;
;当sinx=-1时,ymin=-2
∴实数a的取值范围为
 (12分)
(12分)解二:原方程可化为2sin2x-sinx+a-1=0
令sinx=t,则问题转化为方程2t2-t+a-1=0在[-1,1]内有一解或两解,
设g(t)=2t2-t+a-1,若方程在[-1,1]内有一个解,则
 解得-2≤a<0
解得-2≤a<0若方程在[-1,1]内有两个解,则
 解得
解得
∴实数a的取值范围是[-2,
 ]
]点评:本题考查三角函数的化简求值及一元二次方程的实根分布,本题解题的关键是整理出三角函数的解析式,熟练应用三角函数的公式来解题,本题是一个中档题目.

练习册系列答案
相关题目
 .
.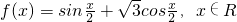 .
. .
.