题目内容
已知函数 .
.(1)化简函数f(x)的解析式,并求其定义域和单调区间;
(2)在△ABC中,角A、B、C所对的边为a,b,c,满足:a2+b2-c2=ab,求f(C)
【答案】分析:(1)利用三角函数的恒等变换化简函数的解析式为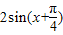 ,题意可得
,题意可得 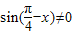 ,
,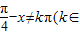 z),由此求得函数的定义域.令 2kπ-
z),由此求得函数的定义域.令 2kπ-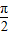 ≤x+
≤x+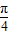 ≤2kπ+
≤2kπ+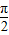 ,k∈z,
,k∈z,
求出x的范围,即可求得函数增区间.令 2kπ+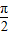 ≤x+
≤x+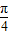 ≤2kπ+
≤2kπ+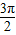 ,k∈z,求出x的范围,即可求得函数的减区间.
,k∈z,求出x的范围,即可求得函数的减区间.
(2)由余弦定理求得cosC的值,可得C的值,从而求得f(C)的值.
解答:解:(1)∵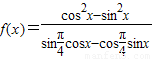 …2分
…2分
=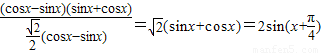 ,…4分
,…4分
由题意可得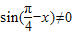 ,∴
,∴ Z),故其定义域为{
Z),故其定义域为{ 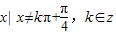 }.…6分
}.…6分
令 2kπ- ≤x+
≤x+ ≤2kπ+
≤2kπ+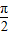 ,k∈z,求得
,k∈z,求得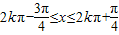 ,k∈z,
,k∈z,
故函数f(x)的增区间为 ,k∈z.
,k∈z.
令 2kπ+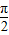 ≤x+
≤x+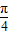 ≤2kπ+
≤2kπ+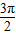 ,k∈z,求得
,k∈z,求得 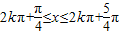 ,k∈z,
,k∈z,
故函数f(x)的减区间为 ,k∈z.
,k∈z.
(2)∵c2=a2+b2-2ab•cosC,由余弦定理可得:cosC=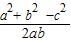 =
= ,
,
∴C=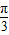 ,∴
,∴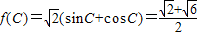 .…12分
.…12分
点评:本题主要考查三角函数的恒等变换及化简求值,两角和差的正弦公式、余弦定理的应用,属于中档题.
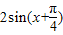 ,题意可得
,题意可得 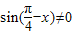 ,
,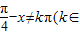 z),由此求得函数的定义域.令 2kπ-
z),由此求得函数的定义域.令 2kπ-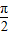 ≤x+
≤x+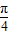 ≤2kπ+
≤2kπ+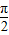 ,k∈z,
,k∈z,求出x的范围,即可求得函数增区间.令 2kπ+
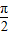 ≤x+
≤x+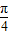 ≤2kπ+
≤2kπ+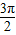 ,k∈z,求出x的范围,即可求得函数的减区间.
,k∈z,求出x的范围,即可求得函数的减区间.(2)由余弦定理求得cosC的值,可得C的值,从而求得f(C)的值.
解答:解:(1)∵
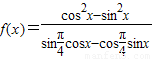 …2分
…2分 =
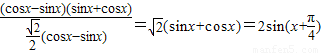 ,…4分
,…4分由题意可得
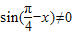 ,∴
,∴ Z),故其定义域为{
Z),故其定义域为{ 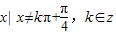 }.…6分
}.…6分令 2kπ-
 ≤x+
≤x+ ≤2kπ+
≤2kπ+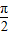 ,k∈z,求得
,k∈z,求得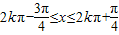 ,k∈z,
,k∈z,故函数f(x)的增区间为
 ,k∈z.
,k∈z.令 2kπ+
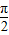 ≤x+
≤x+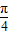 ≤2kπ+
≤2kπ+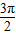 ,k∈z,求得
,k∈z,求得 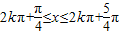 ,k∈z,
,k∈z,故函数f(x)的减区间为
 ,k∈z.
,k∈z.(2)∵c2=a2+b2-2ab•cosC,由余弦定理可得:cosC=
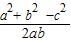 =
= ,
,∴C=
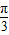 ,∴
,∴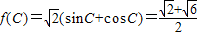 .…12分
.…12分点评:本题主要考查三角函数的恒等变换及化简求值,两角和差的正弦公式、余弦定理的应用,属于中档题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 .
. 上是增函数,求ω的取值范围;
上是增函数,求ω的取值范围;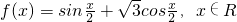 .
. .
.