题目内容
已知函数 .
.(1)化简f(x),并求它的周期;
(2)求f(x)的单调增区间;
(3)该函数的图象经过怎样的变换可以得到y=sinx(x∈R)的图象.
【答案】分析:(1)逆用两角和的正弦公式化简得出f(x)= .
.
(2)将 视为整体,利用正弦函数的单调性求出单调增区间.
视为整体,利用正弦函数的单调性求出单调增区间.
(3)逆向思维解决,将由y=sinx(x∈R)的图象得出 图象的过程逐步逆回即可.
图象的过程逐步逆回即可.
解答:解:(1) =
= ,
,
∴T= =4π.
=4π.
(2)由
得
∴
(3)将 图象上各点的纵坐标缩小为原来的
图象上各点的纵坐标缩小为原来的 倍,横坐标不变得到
倍,横坐标不变得到 的图象,
的图象,
再将 的图象上各点的横坐标缩小到原来的
的图象上各点的横坐标缩小到原来的 倍,纵坐标不变得到
倍,纵坐标不变得到  的图象,
的图象,
再将 的图象向右平移
的图象向右平移 个单位得到y=sinx(x∈R)的图象.
个单位得到y=sinx(x∈R)的图象.
点评:本题考查利用三角函数公式恒等变形转化能力,三角函数的性质,三角函数图象的平移变换,周期变换.考查逆向思维的能力.
 .
.(2)将
 视为整体,利用正弦函数的单调性求出单调增区间.
视为整体,利用正弦函数的单调性求出单调增区间.(3)逆向思维解决,将由y=sinx(x∈R)的图象得出
 图象的过程逐步逆回即可.
图象的过程逐步逆回即可.解答:解:(1)
 =
= ,
,∴T=
 =4π.
=4π.(2)由

得

∴

(3)将
 图象上各点的纵坐标缩小为原来的
图象上各点的纵坐标缩小为原来的 倍,横坐标不变得到
倍,横坐标不变得到 的图象,
的图象,再将
 的图象上各点的横坐标缩小到原来的
的图象上各点的横坐标缩小到原来的 倍,纵坐标不变得到
倍,纵坐标不变得到  的图象,
的图象,再将
 的图象向右平移
的图象向右平移 个单位得到y=sinx(x∈R)的图象.
个单位得到y=sinx(x∈R)的图象.点评:本题考查利用三角函数公式恒等变形转化能力,三角函数的性质,三角函数图象的平移变换,周期变换.考查逆向思维的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
. .
. 上是增函数,求ω的取值范围;
上是增函数,求ω的取值范围;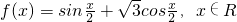 .
.