题目内容
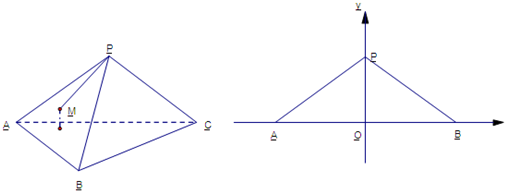
已知正三棱锥P-ABC的侧棱长为2,底面边长为1,平行四边形EFGH的四个顶点分别在棱AB、BC、CP、PA上,则 的最小值为 ________.
的最小值为 ________.
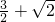
分析:分别设EF=x,FG=y,BF=a,FC=b,由AC:EF=BC:BF,BP:FG=BC:FC可建立模型
 =
= ,再用基本不等式法求得最小值.
,再用基本不等式法求得最小值.解答:
 解:设EF=x,FG=y,BF=a,FC=b
解:设EF=x,FG=y,BF=a,FC=b∵AC:EF=BC:BF,BP:FG=BC:FC
即1:EF=(a+b):a,2:FG=(a+b):b或1:FG=(a+b):2b

=
 ≥
≥
=
 +
+
∴
 的最小值为
的最小值为 +
+
点评:本题主要考查四面体中各点线面的位置关系,同时,还考查了建立模型和解决模型的能力,属中档题.

练习册系列答案
相关题目
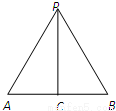
 已知正三棱锥P-ABC主视图如图所示,其中△PAB中,AB=PC=2cm,则这个正三棱锥的左视图的面积为
已知正三棱锥P-ABC主视图如图所示,其中△PAB中,AB=PC=2cm,则这个正三棱锥的左视图的面积为