题目内容
已知全集U=Z,A={-1,0,1,2},B={x|x2=2x},则A∩∁UB= .
考点:交、并、补集的混合运算
专题:集合
分析:解方程化简集合B,然后求∁UB,最后由交集运算得答案.
解答:
解:∵U=Z,B={x|x2=2x}={0,2},
∴∁UB={x∈Z|x≠0,x≠2}.
又A={-1,0,1,2},
则A∩∁UB={-1,1}.
故答案为:{-1,1}.
∴∁UB={x∈Z|x≠0,x≠2}.
又A={-1,0,1,2},
则A∩∁UB={-1,1}.
故答案为:{-1,1}.
点评:本题考查了交、并、补集的混合运算,是基础的计算题.

练习册系列答案
相关题目
“0<k<9”是“曲线
-
=1与曲线
-
=1的焦距相同”的( )
| x2 |
| 25 |
| y2 |
| 9-k |
| x2 |
| 25-k |
| y2 |
| 9 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
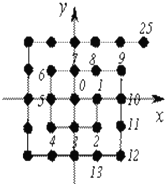 将平面直角坐标系中的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,…,点(0,1)处标7,…,依此类推,则标签20152的格点的坐标为( )
将平面直角坐标系中的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,…,点(0,1)处标7,…,依此类推,则标签20152的格点的坐标为( )| A、(1008,1007) |
| B、(1007,1006) |
| C、(1007,1005) |
| D、(1006,1005) |
下列是映射的是( )


| A、1、2、3 | B、1、2 |
| C、1、3 | D、2、3 |
函数y=
的定义域为( )
| log2(2x2-x) |
A、{x|x≤-
| ||
B、{x|x<-
| ||
C、{x|x≤0,或x≥
| ||
D、{x|x<0,或x>
|
 在四边形ABCD中,
在四边形ABCD中,