题目内容

（2012•珠海一模）口袋中装有完全相同的球7个，2个球标有数字“2”，2个球标有数字“3”，3个球标有数字“4”，第一次从口袋中任意摸出一个球，放回口袋后第二次再任意摸出一个球，记第一次与第二次摸出的球的数字之和为ξ
（Ⅰ）ξ为何值时，其发生的概率最小？说明理由．
（Ⅱ）求随机变量ξ的期望．
分析：（Ⅰ）确定ξ的取值，求出相应的概率，即可得到概率最小时ξ的值；
（Ⅱ）利用数学期望公式，可求随机变量ξ的期望．
解答：解：（Ⅰ）由题设知ξ=4，5，6，7，8
P(ξ=4)=
C
1
2
C
1
2
C
1
7
C
1
7
=
4
49
，P(ξ=5)=
2
C
1
2
C
1
2
C
1
7
C
1
7
=
8
49
，P(ξ=6)=
2
C
1
2
C
1
3
+
C
1
2
C
1
2
C
1
7
C
1
7
=
16
49
，P(ξ=7)=
2
C
1
2
C
1
3
C
1
7
C
1
7
=
12
49
，P(ξ=8)=
C
1
3
C
1
3
C
1
7
C
1
7
=
9
49
，
∴ξ=4时，发生的概率最小．
（Ⅱ）ξ的期望Eξ=4×
4
49
+5×
8
49
+6×
16
49
+7×
12
49
+8×
9
49
=
44
7
点评：本题考查离散型随机变量的概率与期望，考查学生的计算能力，确定变量的取值是关键．
练习册系列答案
相关题目
（2012•珠海一模）若双曲线C：
x2
a2
-
y2
b2
=1(a＞0 ，b＞0)的渐近线为y=±
3
x，则双曲线C的离心率为
2
2
．
（2012•珠海一模）已知复数z的实部是-1，虚部是2，其中i为虚数单位，则
1
z
在复平面对应的点在（　　）
（2012•珠海一模）数列{an}是等差数列，Sn是它的前n项和，若S3=12，S5=30，那么S7=（　　）
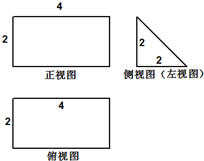（2012•珠海一模）如图，某几何体的正视图和俯视图都是矩形，侧视图是等腰直角三角形，则该几何体的体积为（　　）
（2012•珠海一模）如图，在△ABC中，已知
BC
=3
DC
，则
AD
=（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网